
【题目】定义:如图①,点M、N把线段AB分割成AM、MN和BN,若以AM,MN、BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.
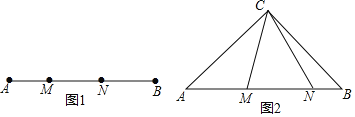
(1)已知点M、N是线段AB的勾股分割点,若AM=2,MN=3,求BN的长;
(2)如图2,在Rt△ABC中,AC=BC,点M,N在斜边AB上,∠MCN=45°,求证:点M,N是线段AB的勾股分割点(提示:把△ACM绕点C逆时针旋转90°)
(3)在(2)的前提下,若∠BCN=15°,BN=1.求AN的长.
【答案】(1)![]() 或
或![]() ;(2)见解析;(3)2+
;(2)见解析;(3)2+![]()
【解析】
(1)分两种情况讨论,根据勾股分割点定义可求BN的长;
(2)过点A作AD⊥AB,且AD=BN,由题意可证△ADC≌△BNC,可得CD=CN,∠ACD=∠BCN,可求∠MCD=∠MCN,则可证△MDC≌△MNC,可得MN=DM,根据勾股定理可得BN2+AM2=MN2,则点M,N是线段AB的勾股分割点;
(3)过点C作CD⊥AB,垂足为D,根据等腰直角三角形的性质可得AD=CD=BD,∠DBC=∠DCB=45°,可求∠DCN=∠DCB﹣∠NCB=30°,可得CD=![]() DN=BD,即可求DN=
DN=BD,即可求DN=![]() ,则可求AN的长.
,则可求AN的长.
(1)分两种情况:
①当MN为最大线段时,
∵点 M、N是线段AB的勾股分割点,
∴BN=![]() ,
,
②当BN为最大线段时,
∵点M、N是线段AB的勾股分割点,
∴BN=![]() ,
,
综上所述:BN的长为![]() 或
或![]() ;
;
(2)如图,过点A作AD⊥AB,且AD=BN,
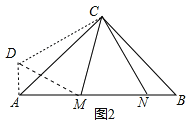
∵AD=BN,∠DAC=∠B=45°,AC=BC,
∴△ADC≌△BNC(SAS),
∴CD=CN,∠ACD=∠BCN,
∵∠MCN=45°,
∴∠DCA+∠ACM=∠ACM+∠BCN=45°,
∴∠MCD=∠MCN,且CD=CN,CM=CM,
∴△MDC≌△MNC(SAS),
∴MN=DM,
在Rt△MDA中,AD2+AM2=DM2,
∴BN2+AM2=MN2,
∴点M,N是线段AB的勾股分割点;
(3)如图,过点C作CD⊥AB,垂足为D,
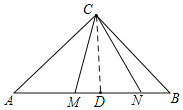
∵AC=BC,∠ACB=90°,CD⊥AB,
∴AD=CD=BD,∠DBC=∠DCB=45°,
∵∠BCN=15°,
∴∠DCN=∠DCB﹣∠NCB=30°,
∵tan∠DCN=![]() ,
,
∴CD=![]() DN,
DN,
∴DB=![]() DN,
DN,
∵NB=DB﹣DN=![]() DN﹣DN=1,
DN﹣DN=1,
∴DN=![]() ,
,
∴AD=DB=![]() DN=
DN=![]() ,
,
∴AN=AD+DN=![]() =2+
=2+![]() .
.


 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
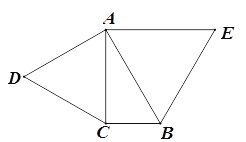
【题目】已知△ABC中, ∠ACB=90°,∠CAB=30°,以AC,AB为边向外作等边三角形ACD和等边三角形ABE,点F在AB上,且到AE,BE的距离相等.
(1)用尺规作出点F; (要求:尺规作图,保留作图痕迹,不写作法)
(2)连接EF,DF,证明四边形ADFE为平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
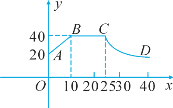
【题目】心理学家研究发现,一般情况下,在一节40分钟的课中,学生的注意力指数y随时间x(分)的变化规律如图所示(其中AB、BC为线段,CD为双曲线的一部分).
(1)分别求出线段AB和双曲线CD的函数解析式,并写出自变量的取值范围;
(2)开始上课后第5分钟时与第30分钟时比较,何时学生的注意力更集中?
(3)一道数学竞赛题,需要讲19分钟,为了效果较好,要求学生的注意力指数至少为36,那么经过适当安排,老师能否在学生达到所需的状态下讲解完这道题目?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
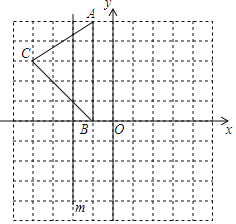
(1)在图中作出△ABC关于m(直线m上的横坐标都为﹣2)的对称图形△A1B1C1;
(2)线段上有一点P(﹣![]() ,
,![]() ),直接写出点P关于直线m对称的点的坐标 .
),直接写出点P关于直线m对称的点的坐标 .
(3)线段BC上有一点M(a,b),点M关于直线m的对称点N(c,d),请直接写出a,c的关系: ;b,d的关系: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C、E和B、D、F分别在∠GAH的两边上,且AB=BC=CD=DE=EF,若∠A=18°,则∠GEF的度数是( )
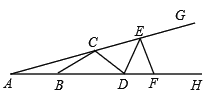
A. 80° B. 90° C. 100° D. 108°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习轴对称的时候,老师让同学们思考课本中的探究题.
如图(1),要在燃气管道l上修建一个泵站,分别向A、B两镇供气.泵站修在管道的什么地方,可使所用的输气管线最短?
你可以在l上找几个点试一试,能发现什么规律?你可以在![]() 上找几个点试一试,能发现什么规律?
上找几个点试一试,能发现什么规律?
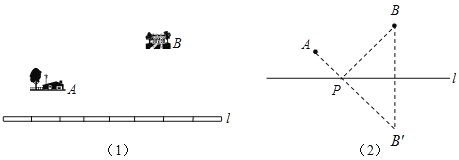
聪明的小华通过独立思考,很快得出了解决这个问题的正确办法.他把管道l看成一条直线(图(2)),问题就转化为,要在直线l上找一点P,使AP与BP的和最小.他的做法是这样的:
①作点B关于直线l的对称点B′.
②连接AB′交直线l于点P,则点P为所求.
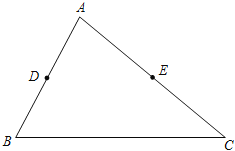
请你参考小华的做法解决下列问题.如图在△ABC中,点D、E分别是AB、AC边的中点,BC=6,BC边上的高为4,请你在BC边上确定一点P,使△PDE得周长最小.
(1)在图中作出点P(保留作图痕迹,不写作法).
(2)请直接写出△PDE周长的最小值:
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的顶点
的顶点![]() 在坐标原点,正方形
在坐标原点,正方形![]() 的边
的边![]() 与
与![]() 在同一直线上,
在同一直线上, ![]() 与
与![]() 在同一直线上,且
在同一直线上,且![]() ,
,![]() 边和
边和![]() 边所在直线的解析式分别为:
边所在直线的解析式分别为: ![]() 和
和![]() ,则点
,则点![]() 的坐标是( )
的坐标是( )
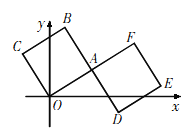
A.(6,-1)B.(7,-1)C.(7,-2)D.(6,-2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2016年“双十一”期间,某快递公司计划租用甲、乙两种车辆快递货物,从货物量来计算:若租用两种车辆合运,10天可以完成任务;若单独租用乙种车辆,完成任务的天数是单独租用甲种车辆完成任务天数的2倍.
(1)求甲、乙两种车辆单独完成任务分别需要多少天?
(2)已知租用甲、乙两种车辆合运需租金65000元,甲种车辆每天的租金比乙种车辆每天的租金多1500元,试问:租甲和乙两种车辆、单独租甲种车辆、单独租乙种车辆这三种租车方案中,哪一种租金最少?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com