
分析 根据|x1-1|+|x2-2|+|x3-3|+…+|x2016-2016|=0,可以求得x1,x2,x3,…,x2016的值,从而可以解答本题.
解答 解:∵|x1-1|+|x2-2|+|x3-3|+…+|x2016-2016|=0,
∴x1-1=0,x2-2=0,x3-3=0,…,x2016-2016=0,
∴x1=1,x2=2,x3=3,…,x2016=2016,
∴2x1-2x2-2x3-…-2x2015+2x2016
=2(x1-x2-x3-…-x2015+x2016)
=2(1-2-3-…-2015+2016)
=2×[2-$\frac{2015(1+2015)}{2}$+2016]
=2×(2-2015×1008+2016)
=2×(2-2031120+2016)
=2×(-2029102)
=-4058204.
点评 本题考查数字的变化类、绝对值,解题的关键是明确题意,找出所求问题需要的条件.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 44×105 | B. | 4.4×106 | C. | 0.44×107 | D. | 4.4×105 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
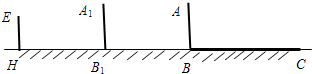 学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为1.6m的小明(AB)的影子BC长是3m,而小颖(EH)刚好在路灯灯泡的正下方H点,并测得HB=6m.
学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为1.6m的小明(AB)的影子BC长是3m,而小颖(EH)刚好在路灯灯泡的正下方H点,并测得HB=6m.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com