练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】下列图形中，既是轴对称图形又是中心对称图形的是（ ）
    A.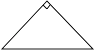
    B.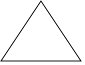
    C.
    D.

    【答案】D
    【解析】解：A、是轴对称图形，不是中心对称图形，故本选项错误；

    B、是轴对称图形，不是中心对称图形，故本选项错误；

    C、不是轴对称图形，是中心对称图形，故本选项错误；

    D、既是轴对称图形又是中心对称图形，故本选项正确．

    所以答案是：D．

    【考点精析】根据题目的已知条件，利用轴对称图形和中心对称及中心对称图形的相关知识可以得到问题的答案，需要掌握两个完全一样的图形关于某条直线对折，如果两边能够完全重合，我们就说这两个图形成轴对称，这条直线就对称轴；如果把一个图形绕着某一点旋转180度后能与另一个图形重合，那么我们就说，这两个图形成中心对称；如果把一个图形绕着某一点旋转180度后能与自身重合，那么我们就说，这个图形成中心对称图形．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，矩形纸片ABCD中，AB=6，AD=10，点P是边BC上的动点，现将纸片折叠，使点A与点P重合，折痕与矩形边的交点分别为E、F，要使折痕始终与边AB、AD有交点，则BP的取值范围是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在下列条件中：①∠A +∠B＝∠C；②∠A：∠B：∠C=l：2：3；③∠A=90°-∠B；④∠A=∠B＝∠C中，能确定△ABC是直角三角形的条件有（ ）

    A. 1个； B. 2个； C. 3个； D. 4个；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下面是某同学对多项式（x2－4x+2）（x2－4x+6）+4进行因式分解的过程．

    解：设x2－4x=y

    原式=（y+2）（y+6）+4 （第一步）

    =y2+8y+16 （第二步）

    =（y+4）2（第三步）

    =（x2－4x+4）2（第四步）

    回答下列问题：

    （1）该同学第二步到第三步运用了因式分解的_______．

    A．提取公因式

    B．平方差公式

    C．两数和的完全平方公式

    D．两数差的完全平方公式

    （2）该同学因式分解的结果是否彻底？________．（填“彻底”或“不彻底”）若不彻底，请直接写出因式分解的最后结果_________ ．

    （3）请你模仿以上方法尝试对多项式（x2－2x）（x2－2x+2）+1进行因式分解．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知直线l1∥l2，l3、l4和l1、l2分别交于点A、B、C、D，点P在直线l3或l4上且不与点A、B、C、D重合．记∠AEP=∠1，∠PFB=∠2，∠EPF=∠3．

    （1）若点P在图（1）位置时，求证：∠3=∠1+∠2；

    （2）若点P在图（2）位置时，请直接写出∠1、∠2、∠3之间的关系；

    （3）若点P在图（3）位置时，写出∠1、∠2、∠3之间的关系并给予证明；

    （4）若点P在C、D两点外侧运动时，请直接写出∠1、∠2、∠3之间的关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，为数轴上两条线段，其中与原点重合，，且．

    （1）当为中点时，求线段的长；

    （2）线段和以（1）中图形为初始位置，同时开展向右运动，线段的运动速度为每秒5个单位长度，线段运动速度为每秒3个单位长度，设运动时间为秒，请结合运动过程解决以下问题：

    ①当时，求的值；

    ②当时，请直接写出的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是我国古代数学家杨辉最早发现的，称为“杨辉三角”，他的发现比西方要早五百年左右，由此可见我国古代数学的成就是非常值得中华民族自豪的。“杨辉三角”中有许多规律，如它的每一行的数字正好对应了(a+b)n（n为非负整数）的展开式中a按次数从大到小排列的项的系数，例如：(a+b)2=a2+2ab+b2展开式中的系数1,2,1恰好对应图中第三行的数字；(a+b)3=a3+3a2b+3ab2+b3展开式中的系数1,3,3,1恰好对应图中第四行的数字…….请认真观察此图，根据前面各式的规律，写出(a+b)6的展开式：(a+b)6=____.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】直接写出结果：（1）－1＋1＝_____；（2）3－7＝_____；

    （3）4÷＝_____；（4）－7×0.5＝_____；（5）(－2)3＝_____；

    （6）(－1)2n＝_______（n为正整数）；（7）4x＝0的解是_____；

    （8）x＝4 的解是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某公司有330台机器要运送到外地，计划租用甲、乙两种货车．已知甲种货车每辆租金400元，乙种货车每辆租金280元，若租用3辆甲种货车和2辆乙种货车，可运送195台机器；若租用4辆甲种货车和1辆乙种货车，可运送210台机器；
    （1）求每辆甲种货车和乙种货车能运送的机器数量；
    （2）请给出一次性将机器运送到目的地的最节省费用的租车方案，并说明理由．

    查看答案和解析>>

    同步练习册答案