
【题目】如图,在坡顶B处的同一水平面上有一座纪念碑CD垂直于水平面,小明在斜坡底A处测得该纪念碑顶部D的仰角为45°,然后他沿着坡比i=5:12的斜坡AB攀行了39米到达坡顶,在坡顶B处又测得该纪念碑顶部的仰角为68°.求坡顶B到地面AE的距离和纪念碑CD的高度.(结果精确到1米,参考数据:sin68°=0.9,cos68°=0.4,tan68°=2.5)
【答案】解:过点B作BG⊥AE,垂足为点G,如图.
∵i=tan∠BAG= ![]() =5:12,
=5:12,
∴设BG=5k,则AG=12k,
在Rt△BAG中,由勾股定理得,AB=13k,
∴13k=39,解得k=3,
∴BG=15,
∴坡顶B到AE的距离为15米.
延长DC交AE于点F,
∵BC⊥DC,BC∥AE,
∴DF⊥AE,
∴四边形BCFG是矩形,CF=BG=15,BC=GF,
∵∠DAF=45°,
∴AF=DF,
设DC=x,则AF=36+GF,DF=x+15,即x+15=35+GF,
∴BC=GF=x﹣21,
在Rt△DBC中,tan∠DBC= ![]() ,即
,即 ![]() ≈2.5,
≈2.5,
解得x≈35,
答:坡顶B到地面AE的距离为15米,纪念碑CD的高度约为35米.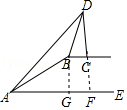
【解析】过点B作BG⊥AE,垂足为点G,如图.根据已知条件得到设BG=5k,则AG=12k,在Rt△BAG中,由勾股定理得,AB=13k,得到BG=15,于是得到坡顶B到AE的距离为15米.延长DC交AE于点F,根据平行线的性质得到DF⊥AE,根据矩形的性质得到AF=DF,设DC=x,则AF=36+GF,DF=x+15,得到BC=GF=x﹣21,根据三角函数的定义即可得到结论.
【考点精析】本题主要考查了关于坡度坡角问题和关于仰角俯角问题的相关知识点,需要掌握坡面的铅直高度h和水平宽度l的比叫做坡度(坡比).用字母i表示,即i=h/l.把坡面与水平面的夹角记作A(叫做坡角),那么i=h/l=tanA;仰角:视线在水平线上方的角;俯角:视线在水平线下方的角才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】给出下面两个定理:
①线段垂直平分线上的点到这条线段两个端点的距离相等;
②到一条线段两个端点距离相等的点在这条线段的垂直平分线上.
应用上述定理进行如下推理:
如图,直线l是线段MN的垂直平分线.

∵点A在直线l上,∴AM=AN.( )
∵BM=BN,∴点B在直线l上.( )
∵CM≠CN,∴点C不在直线l上.
这是∵如果点C在直线l上,那么CM=CN, ( )
这与条件CM≠CN矛盾.
以上推理中各括号内应注明的理由依次是 ( )
A. ②①① B. ②①②
C. ①②② D. ①②①
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年我区的葡萄喜获丰收,葡萄一上市,水果店的王老板用2400元购进一批葡萄,很快售完;老板又用5000元购进第二批葡萄,所购件数是第一批的2倍,但进价比第一批每件多了5元.
(1)第一批葡萄每件进价多少元?
(2)王老板以每件150元的价格销售第二批葡萄,售出80%后,为了尽快售完,决定打折促销,要使第二批葡萄的销售利润不少于640元,剩余的葡萄每件售价最少打几折?(利润=售价-进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,BC=4,以顶点A,B为圆心,以AD、BC长为半径作两条弧,两弧相切于点E,且E在AB上,以AB为直径作半圆恰好与DC相切,则图中阴影部分的面积为 . 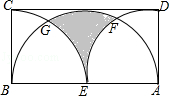
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织七年级全体学生举行了“汉字听写”比赛,每位学生听写汉字39个,随机抽取了部分学生的听写结果,绘制成如下的图表.
组别 | 正确字数x | 人数 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | n |

根据以上信息完成下列问题:
(1)由统计表可知m+n= ,并补全条形统计图.
(2)扇形统计图中“C组”所对应的圆心角的度数是 .
(3)已知该校七年级共有900名学生,如果听写正确的字的个数少于24个定为不合格,请你估计该年级本次听写比赛不合格的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长江是我们的母亲河,金港新区为了打造沿江风景,吸引游客搞活经济,将一段长为180米的沿江河道整治任务交由A、B两工程队先后接力完成.A工作队每天整治12米,B工程队每天整治8米,共用时20天.求A、B两工程队分别整治河道多少米?
⑴根据题意,七⑴班甲同学列出尚不完整的方程组如下。根据甲同学所列的方程组,请你分别指出未知数x、y表示的意义,然后在方框中补全甲同学所列的方程组;
![]() ,x表示________________________,y表示_________________________;
,x表示________________________,y表示_________________________;
⑵如果乙同学直接设A工程队整治河道的米数为x,B工程队整治河道的米数为y,列出了一个方程组,求A、B两工程队分别整治河道多少米.请你帮助他写出完整的解答过程。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,若点P(x,y)的坐标x、y均为整数,则称点P为格点,若一个多边形的面积记为S,其内部的格点数记为N,边界上的格点数记为L,例如图中△ABC是格点三角形,对应的S=1,N=0,L=4.
(1)求出图中格点四边形DEFG对应的S,N,L.
(2)已知格点多边形的面积可表示为S=N+aL+b,其中a,b为常数,若某格点多边形对应的N=82,L=38,求S的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:四条边都相等且四个角都是直角的四边形叫做正方形。我校“快乐走班”数学兴趣小组开展了一次课外活动,过程如下:如图①,正方形ABCD中,AB=6,将三角板放在正方形ABCD上,使三角板的直角顶点与D点重合.三角板的一边交AB于点P,另一边交BC的延长线于点Q.

(1)求证:DP=DQ;
(2)如图②,小明在图1的基础上作∠PDQ的平分线DE交BC于点E,连接PE,他发现PE和QE存在一定的数量关系,请猜测他的结论并予以证明;
(3)如图③,固定三角板直角顶点在D点不动,转动三角板,使三角板的一边交AB的延长线于点P,另一边交BC的延长线于点Q,仍作∠PDQ的平分线DE交BC延长线于点E,连接PE,若AB:AP=3:4,请帮小明算出△DEP的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,CE、BE的交点为E,现作如下操作:
第一次操作,分别作∠ABE和∠DCE的平分线,交点为E1,
第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为E2,
第三次操作,分别作∠ABE2和∠DCE2的平分线,交点为E3,…,
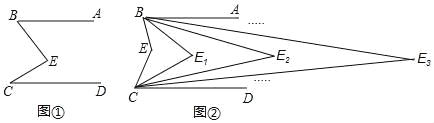
第n次操作,分别作∠ABEn﹣1和∠DCEn﹣1的平分线,交点为En.
(1)如图①,求证:∠BEC=∠ABE+∠DCE;
(2)如图②,求证:∠BE2C=![]() ∠BEC;
∠BEC;
(3)猜想:若∠En=α度,那∠BEC等于多少度?(直接写出结论).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com