
����Ŀ����֪������y��x2��2ax+m��
��1����a��2��m����5ʱ���������ߵ���ֵ��
��2����a��2ʱ�����������������������������㣬������y������ƽ��k����λ���Ⱥõ��µ���������x��û�н��㣬���ж�k��ȡֵ�������˵�����ɣ�
��3����m��0ʱ��ƽ����y���ֱ��l�ֱ���ֱ��y��x����a��1���������߽���P��Q���㣮��ƽ��ֱ��l������ʹ��P��Q����x����·�����a��ȡֵ��Χ��
���𰸡���1��-9����2��k��0������������3��a��1��a����1
��������
(1)��a��2��m����5���������߽���ʽ�����������ߵ���ֵ��
(2)��a��2���룬���������������������������㣬����������x�ᡢy��ֱ���һ���������������x�ᡢy�ύ��ԭ�㣬�ֱ����m��ֵ��������y������ƽ��k����λ���ȣ��õ��µ���������x��û�н��㣬�г�����ʽ�������ж�k��ȡֵ��
(3)�������⣬��a����0��aС��0����������ۼ��ɵ�a��ȡֵ��Χ��
�⣺(1)��a��2��m����5ʱ��
y��x2��4x��5
����x��2��2��9
���������ߵ���СֵΪ��9��
(2)��a��2ʱ��
y��x2��4x+m
��Ϊ�������������������������㣬
�ٸ���������x�ᡢy��ֱ���һ������
���=16-4m=0��
��m=4��
��y��x2��4x+4=��x-2��2
��y������ƽ��k����λ���Ⱥõ��µ���������x��û�н��㣬
��k��0��
�ڸ���������x�ᡢy�ύ��ԭ�㣬
��m=0��
��y��x2��4x
�߰�����y������ƽ��k����λ���Ⱥõ��µ���������x��û�н��㣬
��y��x2��4x+k
��ʱ����0��
��16��4k��0
���k��4;
���ϣ�k��0ʱ��������y������ƽ��k����λ���Ⱥõ��µ���������x��û�н��㣻
(3)��m��0ʱ��y��x2��2ax
�����߿������ϣ���x�ύ������Ϊ��0��0����2a��0����a��0��
ֱ��l�ֱ���ֱ��y��x����a��1���������߽���P��Q���㣬
ƽ��ֱ��l������ʹ��P��Q����x����·���
����a��0ʱ����ͼ1��ʾ��
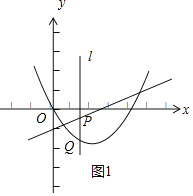
��ʱ����x��0ʱ��0��a+1��0�����a��1��
����a��0ʱ����ͼ2��ʾ��
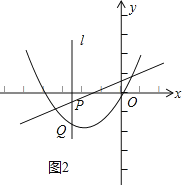
��ʱ����x��2aʱ��2a��a+1��0�����a����1��
���ϣ�a��1��a����1��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
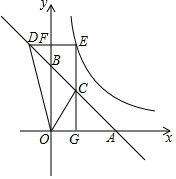
����Ŀ����ͼ����ֱ֪��l��y����x+4�ֱ���x�ᡢy�ύ�ڵ�A��B��˫����![]() ��k��0��x��0����ֱ��l���ཻ��EΪ˫������һ���㣬����E��EG��x���ڵ�G��EF��y���ڵ�F���ֱ���ֱ��l���ڵ�C��D���ҡ�COD��45�㣬��k��_____��
��k��0��x��0����ֱ��l���ཻ��EΪ˫������һ���㣬����E��EG��x���ڵ�G��EF��y���ڵ�F���ֱ���ֱ��l���ڵ�C��D���ҡ�COD��45�㣬��k��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ����������̨![]() �͵��Ժ�
�͵��Ժ�![]() �ʹ�ӡ��.�������1̨
�ʹ�ӡ��.�������1̨![]() �͵��ԣ�2̨
�͵��ԣ�2̨![]() �ʹ�ӡ����һ����Ҫ����6200Ԫ���������2̨
�ʹ�ӡ����һ����Ҫ����6200Ԫ���������2̨![]() �͵��ԣ�1̨
�͵��ԣ�1̨![]() �ʹ�ӡ����һ����Ҫ����7900Ԫ��
�ʹ�ӡ����һ����Ҫ����7900Ԫ��
��1����ÿ̨![]() �͵��Ժ�ÿ̨
�͵��Ժ�ÿ̨![]() �ʹ�ӡ���ļ۸�ֱ��Ƕ���Ԫ��
�ʹ�ӡ���ļ۸�ֱ��Ƕ���Ԫ��
��2�����ѧУ����![]() �͵��Ժ�
�͵��Ժ�![]() �ʹ�ӡ����Ԥ����ò�����20000Ԫ�����ҹ���
�ʹ�ӡ����Ԥ����ò�����20000Ԫ�����ҹ���![]() �ʹ�ӡ����̨��Ҫ�ȹ���
�ʹ�ӡ����̨��Ҫ�ȹ���![]() �͵��Ե�̨����1̨����ô��ѧУ�����ܹ������̨
�͵��Ե�̨����1̨����ô��ѧУ�����ܹ������̨![]() �ʹ�ӡ����
�ʹ�ӡ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() �Ե�
�Ե�![]() ΪԲ�ģ������ⳤΪ�뾶�����ֱ�
ΪԲ�ģ������ⳤΪ�뾶�����ֱ�![]() ��
��![]() ��
��![]() ���㣬�ٷֱ��Ե�
���㣬�ٷֱ��Ե�![]() ΪԲ�ģ��Դ���
ΪԲ�ģ��Դ���![]() �ij�Ϊ�뾶�������ڵ�
�ij�Ϊ�뾶�������ڵ�![]() ��������
��������![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() �������
�������![]() ���������__________��
���������__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
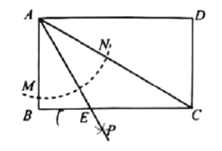
����Ŀ����ͼ��P�ǵ���ֱ����ABC��һ�㣬��BP�Ƶ�B˳ʱ����ת90����BP����ʹ��P������ABC�ڣ���֪��AP��B��135����������P��C��P��A��P��C��1��4����P��A��P��B����������
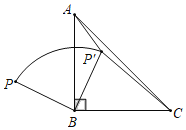
A.1��4B.1��5C.2��![]() D.1��
D.1��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��A������Ϊ��4��0������B������Ϊ��0��3�����ڵ�һ��������һ��P(a,b) ,ʹ��PABΪ�ȱ������Σ���2(a-b)=___________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı���OABC�Ķ���O��B��y���ϣ�����A�ڷ���������y����![]() �ϣ�����C�ڷ���������y��
�ϣ�����C�ڷ���������y��![]() �ϣ���ƽ���ı���OABC�������(����)
�ϣ���ƽ���ı���OABC�������(����)
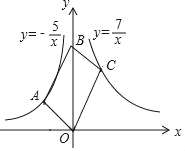
A.8B.10C.12D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() ��
��![]() ���ڵ�
���ڵ�![]() ����
����![]() ���ڵ�
���ڵ�![]() ��������
��������![]() ������
������![]() ����
����![]() ���ڵ�
���ڵ�![]() ����
����![]() Ϊ��������һ���㣬����
Ϊ��������һ���㣬����![]() ��
��![]() ��Ĵ��ߣ���ֱ��
��Ĵ��ߣ���ֱ��![]() �ڵ�
�ڵ�![]() �����
�����![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() .
.

��1���������ߵĽ���ʽ.
��2������![]() ��ֱ��
��ֱ��![]() �·������������˶�ʱ�����
�·������������˶�ʱ�����![]() ���ȵ����ֵ.
���ȵ����ֵ.
��3������![]() ��
��![]() ��
��![]() Ϊ������������ǵ���������ʱ�����ʱ
Ϊ������������ǵ���������ʱ�����ʱ![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����С����һ����Ϸ�����Ŵ�С���ʵض���ͬ�Ŀ�Ƭ�Ϸֱ��������2��3��4��������ȫ��ͬ�����ֽ��������ֵ�һ�泯�£�С�����������ȡһ�ţ��������ֺ�Ż�ϴ�ȣ�Ȼ��С�����������ȡһ�ţ�����С����С����õ���������֮�ͣ�����Ϊ��������С��ʤ������Ϊż������С��ʤ��
��1�������û���״ͼ���б��ķ����������������Ϊ6�ĸ��ʣ�
��2������Ϊ�����Ϸ�����˫����ƽ��˵˵������ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com