
����Ŀ��ͬѧ�ǣ���ѧ��Դ�������ַ��������������ѧ�е�֪ʶ���������ǽ������ʵ������.�������뽨һ�����У������鷢�����Ҹ�����������ľ�����![]() ��
��![]() ��ͬʱ�����ཻ��������·
��ͬʱ�����ཻ��������·![]() ��
��![]() ��Ϊ��������;������������ѳ��н��ڵ����������ľ�����ȣ�ͬʱ������·����Ҳ��ȵ�λ���ϣ����������µľ�������·��λ��ͼ.��������һ��������ѧ����ѧ֪ʶ����������ͼ��ȷ�����е�λ�ã������߹���ͼȷ�����е�
��Ϊ��������;������������ѳ��н��ڵ����������ľ�����ȣ�ͬʱ������·����Ҳ��ȵ�λ���ϣ����������µľ�������·��λ��ͼ.��������һ��������ѧ����ѧ֪ʶ����������ͼ��ȷ�����е�λ�ã������߹���ͼȷ�����е�![]() ��λ��.(��ͼ��д��������Ҫ������ͼ�ۼ�)
��λ��.(��ͼ��д��������Ҫ������ͼ�ۼ�)
�Ƚ�ʵ������ת��Ϊ��ѧ���⣬�ѳ��п���һ����.
��![]() ��
��![]() ��
��![]() ����ľ�����ȣ��������ʣ�__________________�� ���ó߹�����_____________���ֵ�
����ľ�����ȣ��������ʣ�__________________�� ���ó߹�����_____________���ֵ�![]() �����ֱཻ��
�����ֱཻ��![]() ��
��![]() �ľ�����ȣ��������ʣ�_________________�� ���ó߹�����_______________������
�ľ�����ȣ��������ʣ�_________________�� ���ó߹�����_______________������![]() ͬʱ���������������������Ӧ�������ǵĽ���.
ͬʱ���������������������Ӧ�������ǵĽ���.
��ͬѧ������ɷ�������(�����) ������ͼ��

���𰸡���ͼ��ʾ������. �߶δ�ֱƽ�����ϵĵ㵽�߶������˵�ľ�����ȣ��߶�![]() �Ĵ�ֱƽ���ߣ���ƽ�����ϵĵ㵽�����ߵľ�����ȣ�
�Ĵ�ֱƽ���ߣ���ƽ�����ϵĵ㵽�����ߵľ�����ȣ�![]() �Ľ�ƽ����.
�Ľ�ƽ����.
��������
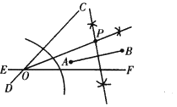
�����߶δ�ֱƽ�����ϵĵ㵽�߶����˵�ľ�����ȣ���ƽ�����ϵĵ㵽�ǵ����ߵľ�����ȵ����ʣ��ֱ�����AB�Ĵ�ֱƽ���ߣ��ֱཻ�����ɼнǵ�ƽ���ߣ������ཻ�ڵ�P�����P��Ϊ��Ҫ�����ij��е�λ�ã�
��ͼ��ʾ��
�߶δ�ֱƽ�����ϵĵ㵽�߶������˵�ľ������
�߶�![]() �Ĵ�ֱƽ����
�Ĵ�ֱƽ����
��ƽ�����ϵĵ㵽�����ߵľ������
![]() �Ľ�ƽ����
�Ľ�ƽ����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABE�У�E 90��AC ��BAE�Ľ�ƽ���ߡ�
��1����B 30����BAC�Ķ�����
��2���� D ��BC���е㣬��ABC�����Ϊ24��CD3����AE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ı���ABCD�������ϵ��е�ֱ�ΪE��F��G��H��˳������EF��FG��GH��HE���õ��ı���EFGH�����ı���ABCD���е��ı��Σ���
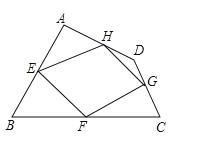
��1���ı���EFGH����״��ʲô����֤����Ľ��ۣ�
��2�����ı���ABCD�ĶԽ�������ʲô����ʱ���ı���EFGH�Ǿ��Σ��������������������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijʡ�ƻ�5����ȫ���ؼ���ͨ����.ij������̩�ݾ��ڵĽ��輴��չ�������д�����ɳʯ��Ҫ����.ij������������Ϊ8t��10t�Ŀ�����12����ȫ����������һ��������100tɳʯ.
��1����ij����������Ϊ8t��10t�Ŀ������ж�������
��2�����Ź��̵Ľ�չ��ij������Ҫһ������ɳʯ165t����,Ϊ����������������������ֿ�����7���������ж����ֹ���?����һһ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
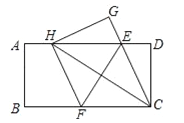
����Ŀ����ͼ����һ�ž���ֽƬABCD����AB=4��BC=8����E��F�ֱ���AD��BC������ֽƬABCD��ֱ��EF�۵�����C����AD�ϵ�һ��H������D���ڵ�G�����������ĸ�������
���ı���CFHE�����������߶�BF��ȡֵ��ΧΪ3��BF��4��
��ECƽ����DCH��������H���A�غ�ʱ��EF=![]() ��
��
���Ͻ�����������Ϊ��ȷ����______��������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ı���ABCD�������Σ���P��ֱ��BC�ϣ���G��ֱ��AD�ϣ�P��G���������ζ����غϣ�����CD��ͬ�ࣩ��PD=PG��DF��PG�ڵ�H����ֱ��AB�ڵ�F�����߶�PG�Ƶ�P��ʱ����ת90���õ��߶�PE������EF��
��1����ͼ1������P���G�ֱ����߶�BC���߶�AD��ʱ��
����ֱ��д���߶�DG��PC��������ϵ(��Ҫ��֤������
����֤���ı���PEFD�����Σ�
��2����ͼ2������P���G�ֱ����߶�BC���߶�AD���ӳ�����ʱ��������ı���PEFD�������������ı��Σ���֤����IJ��룮


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,������1����2����ô���������κ�һ����������1��![]() ����2��
����2��![]() ����3����B����D����4����C����AED�� �������ж���ABC�ס�ADE�ĸ���Ϊ
����3����B����D����4����C����AED�� �������ж���ABC�ס�ADE�ĸ���Ϊ

A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AD��AB������E��BC��һ�㣬��DE=DA��AF��DE������Ϊ��F�������н����У���һ����ȷ���ǣ�������
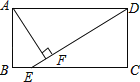
A. ��AFD�ա�DCE B. AF=![]() AD C. AB=AF D. BE=AD��DF
AD C. AB=AF D. BE=AD��DF
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��Rt��ABC�У���ABC=90�㣬��D��BC�ߵ��е㣬�ֱ���B��CΪԲ�ģ������߶�BC����һ��ij�Ϊ�뾶Բ����������ֱ��BC�Ϸ��Ľ���ΪP��ֱ��PD��AC�ڵ�E������BE�������н��ۣ���ED��BC���ڡ�A=��EBA����EBƽ����AED����ED=![]() AB�У�һ����ȷ������ ��
AB�У�һ����ȷ������ ��

A���٢ڢ� B���٢ڢ� C���٢ۢ� D���ڢۢ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com