

���� ��1�����ڵ�P�ӵ�D����������ͼ����S��t��ͼ���֪����P��˳ʱ�뷽���������OABCD�ı��������˶������˶��ٶ�Ϊ1����λ����/�룬����DC=5��BC=5��AB=2��AO=8��OD=6���ɴ˵õ���C�����꣬��ͼ��20-12=8���ó�B�����ꣻ
��2���������G���꣬���ô���ϵ�������������
��3������������OABCD������͡�OCP��������ٷ����������������
�ٵ�P��CD��ʱ��CP=5-t���ɡ�OCP������ó�t��ֵ�����ɵó�P�����ꣻ
�ڵ�P��OA��ʱ����P��x��0�����ɡ�OCP������ó�x��ֵ�����ɵó�P�����ꣻ
�۵�P��BC��ʱ�����㣨$\frac{14}{3}$��0����OCƽ����l��BC��P�����ֱ��OC���㣨$\frac{14}{3}$��0����OCƽ�е�ֱ��l�Լ�ֱ��BC�Ľ���ʽ��l��BC�Ľ��㼴ΪP���ⷽ���鼴�ɣ�
��� �⣺��1�������⣬��֪��P���˶�·���ǣ�D��C��B��A��O��D��
DC=5��BC=10-5=5��AB=12-10=2��AO=20-12=8��OD=26-20=6��
���C��������5��6����
��ͼ�ڣ�20-12=8��
���B��������8��2����
��2����GH�Ľ���ʽΪy=kx+b��
�ߵ���P�˶���Bʱ��S=$\frac{1}{2}$��6��8=24��
��G��12��24����
�ѵ�G��12��24����H��20��0������ã�$\left\{\begin{array}{l}{12k+b=24}\\{20k+b=0}\end{array}\right.$��
��ã�k=-3��b=60��
��ͼ����GH����ֱ�ߵĽ���ʽΪ��y=-3x+60��
��3�����ڵ�P��ʹ��OCP�����Ϊ�����OABCD�������$\frac{1}{3}$�������������
��CM��OA��M����ͼ����ʾ�� �������OABCD�����=����ODCM�����+����ABCM�����=5��6+$\frac{1}{2}$��2+6����8-5��=42��
�������OABCD�����=����ODCM�����+����ABCM�����=5��6+$\frac{1}{2}$��2+6����8-5��=42��
��OCP�����=$\frac{1}{3}$��42=14��
�����������
����ͼ��ã���P��CD��ʱ��CP=5-t����OCP�����=$\frac{1}{2}$��5-t����6=14��
��ã�t=$\frac{1}{3}$��
��P��$\frac{1}{3}$��6����
���ɢٵã���P��OA��ʱ����P��x��0����
���OCP�����=$\frac{1}{2}$x��6=14��
��ã�x=$\frac{14}{3}$��
��P��$\frac{14}{3}$��0����
�۵�P��BC��ʱ�����㣨$\frac{14}{3}$��0����OCƽ����l��BC��P����ͼ����ʾ��
��ֱ��OCΪy=$\frac{6}{5}$x����ֱ��l�Ľ���ʽΪy=$\frac{6}{5}$x+b��
�ѵ㣨$\frac{14}{3}$��0������ã�b=-$\frac{28}{5}$��
��l�Ľ���ʽΪ��y=$\frac{6}{5}$x-$\frac{28}{5}$��
��ֱ��BC�Ľ���ʽΪy=ax+c��
��B��8��2����C��5��6������ã�$\left\{\begin{array}{l}{8k+b=2}\\{5k+b=6}\end{array}\right.$��
��ã�k=-$\frac{4}{3}$��b=$\frac{38}{3}$��
��ֱ��BC�Ľ���ʽΪ��y=-$\frac{4}{3}$x+$\frac{38}{3}$��
�ⷽ����$\left\{\begin{array}{l}{y=\frac{6}{5}x-\frac{28}{5}}\\{y=-\frac{4}{3}x+\frac{38}{3}}\end{array}\right.$�ã�$\left\{\begin{array}{l}{x=\frac{137}{19}}\\{y=\frac{174}{57}}\end{array}\right.$��
��P��$\frac{137}{19}$��$\frac{174}{57}$������P��OD��ʱ��5OP=14��2��OP=5.6��
��P��0��5.6��
������������P��������$\frac{1}{3}$��6������$\frac{14}{3}$��0������$\frac{137}{19}$��$\frac{174}{57}$������0.5.6����
���� ������һ�κ����ۺ��⣬�����˵�����ꡢ�ô���ϵ������һ�κ����Ľ���ʽ��ͼ������ļ��㣬�����������֪ʶ�������ѶȽϴ��ۺ���ǿ���ر��ǣ�3������������ۣ�ͨ���������߲��ܵó������


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
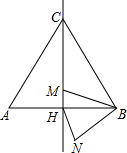 ��ͼ���߳�Ϊ5�ĵȱ�������ABC�У�M�Ǹ�CH����ֱ���ϵ�һ�����㣬����MB�����߶�BM�Ƶ�B��ʱ����ת60��õ�BN������HN�����ڵ�M�˶������У��߶�HN���ȵ���Сֵ��1.25��
��ͼ���߳�Ϊ5�ĵȱ�������ABC�У�M�Ǹ�CH����ֱ���ϵ�һ�����㣬����MB�����߶�BM�Ƶ�B��ʱ����ת60��õ�BN������HN�����ڵ�M�˶������У��߶�HN���ȵ���Сֵ��1.25���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=$\frac{{x}^{2}}{4}$+1 | B�� | y=x2+2x+1 | C�� | y=2x2+1 | D�� | y=x2+1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��?ABCD�У�AC��AB��AB=3cm��BC=5cm����EΪAB��һ�㣬��AE=$\frac{1}{3}$AB����P��B���������1cm/s���ٶ���BC��CD��DA�˶���A��ֹͣ�����˶�ʱ��Ϊ$\frac{5}{3}$��2��$\frac{12}{5}$��$\frac{{68-2\sqrt{21}}}{5}$��ʱ����BEPΪ���������Σ�
��ͼ��?ABCD�У�AC��AB��AB=3cm��BC=5cm����EΪAB��һ�㣬��AE=$\frac{1}{3}$AB����P��B���������1cm/s���ٶ���BC��CD��DA�˶���A��ֹͣ�����˶�ʱ��Ϊ$\frac{5}{3}$��2��$\frac{12}{5}$��$\frac{{68-2\sqrt{21}}}{5}$��ʱ����BEPΪ���������Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
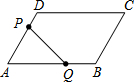 ��ͼ����ƽ���ı���ABCD�У�AB=8cm��AD=4cm����A=60�㣬����P��2cm/s���ٶȴ�D���A�ƶ�������Q��4cm/s���ٶȴӵ�A���B�ƶ������P��Q����ֱ��D��Aͬʱ��������һ�������յ�ʱ����ֹ֮ͣ�˶�����ô����1�룬�����PQBCD�����С��
��ͼ����ƽ���ı���ABCD�У�AB=8cm��AD=4cm����A=60�㣬����P��2cm/s���ٶȴ�D���A�ƶ�������Q��4cm/s���ٶȴӵ�A���B�ƶ������P��Q����ֱ��D��Aͬʱ��������һ�������յ�ʱ����ֹ֮ͣ�˶�����ô����1�룬�����PQBCD�����С���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com