
����Ŀ����֪������L1��y1��x2��6x��5k��������L2��y2��kx2��6kx��5k������k��0��
(1)����˵������Ϊ��ȷ����(��д���) ��
��������L1��L2��y�ύ��ͬһ��(0��5k)��
��������L1��L2���ڶ����ϣ�
��������L1��L2�ĶԳ�����ͬһ��ֱ�ߣ�
�ܵ�k����1ʱ��������L1��L2����x�����������㣮
(2)������L1��L2�ཻ�ڵ�E��F����k��ֵ�����仯ʱ�����ж��߶�EF�ij����Ƿ����仯����˵�����ɣ�
(3)��(2)�У���������L1�Ķ���ΪM��������L2�Ķ���ΪN�����Ƿ����ʵ��k��ʹMN��2EF������ڣ����ʵ��k���粻���ڣ���˵�����ɣ�
���𰸡�(1) �٢ۢܡ�;(2)������;(3)������.
��������
��1�����ݶ��κ�����ͼ������ʽ����֪���������жϼ��ɣ�
��2����y1=y2�ɵ÷�����x2+6x+5k= kx2+6kx+5k����˷��̿ɵ�![]() ���ɴ˿ɵ��������ߵĽ�������ֱ�Ϊ��0��5k���ͣ�-6��5k�����Ӷ��ɵ�EF=0-��-6��=6����EF�ij��Ȳ�����k�ı仯���仯��
���ɴ˿ɵ��������ߵĽ�������ֱ�Ϊ��0��5k���ͣ�-6��5k�����Ӷ��ɵ�EF=0-��-6��=6����EF�ij��Ȳ�����k�ı仯���仯��
��3����������������ʽ�䷽������õ�M��N�����꣬�Ӷ��ú�k�Ĵ���ʽ�����MN�ij����������2��������EF=6�����г�����k�ķ��̣���˷��̼��ɵõ���Ӧ�Ľ���.
(1)�١���������L1��y1��x2��6x��5k��������L2��y2��kx2��6kx��5k������x=0ʱ��y1=y2=5k��
��������L1��L2����y���ཻ�ڵ㣨0��5k��������������ȷ��
����������L1��y1��x2��6x��5k�Ŀ�����������������L2��y2��kx2��6kx��5k�Ŀ��ڷ���ȷ����
�ࡰ������L1��L2���ڶ����ϡ���˵���Ǵ����������������������
����������L1��y1��x2��6x��5k�ĶԳ���Ϊֱ��x=-3��������L2��y2��kx2��6kx��5k�ĶԳ���ҲΪֱ��x=-3��
�ࡰ������L1��L2�ĶԳ�����ͬһ��ֱ�ߡ���˵������ȷ�ģ������ۢ۳�����
������������L1��y1��x2��6x��5k������=36-20k��
����k<-1ʱ����>0����ʱ������L1��x����������ͬ�Ľ��㣻
����������L2��y2��kx2��6kx��5k������=16k2��
����k<-1ʱ����>0����ʱ������L2��x����������ͬ�Ľ��㣻
����k<-1ʱ�����������߶���x����������ͬ�Ľ��㣬�ʽ�����������
������������ȷ����������٢ۢܡ���
(2) ��y1= y2���ɵã�x2+6x+5k= kx2+6kx+5k��
��ã�x1=0��x2=��6��
����x=0��x=-6ʱ��y1=y2=5k��
���������ߵĽ�������Ϊ(0��5k)��(��6��5k)��
��EF��0��(��6)=6��
����k��ֵ�����仯ʱ���߶�EF�ij��Ȳ��ᷢ���仯��
(3)����ʵ��k��ʹMN=2EF������������
��y1=x2+6x+5k=(x+3)2��9+5k��y2=kx2+6kx+5k=k(x+3)2��4k��
��������L1�Ķ���M����Ϊ(��3����9+5k)��������L2�Ķ���N����Ϊ(��3����4k)��
��MN=![]() ��
��
��MN=2EF��EF=6��
��![]() ��
��
��ã�k1=![]() ��k2=
��k2=![]() ��
��
������ʵ����k1=![]() ��k2=
��k2=![]() ʹMN=2EF.
ʹMN=2EF.


 ����Ӣ��ϵ�д�
����Ӣ��ϵ�д� ����ѧУ�ֲ����ܲ�ϵ�д�
����ѧУ�ֲ����ܲ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����·��A��B�������25 km��C��DΪ����ׯ��DA��AB�ڵ�A��CB��AB�ڵ�B����֪DA��15 km��CB��10 km������Ҫ����·AB�Ͻ�һ�����ز�Ʒ�չ�վE��ʹ��C��D���嵽Eվ�ľ�����ȣ���EվӦ������Aվ����km����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����мס��ҡ����ȶ��ʳƷ��˾��ij�п��走��꣬���е��������������ͳ��ͼ��ͼ��ʾ������ͳ��ͼ��û�б�ע��Ӧ��˾�����İٷֱȣ���֪�ҹ�˾��Ӫ150�ҵ���꣬����ݸ�ͳ��ͼ�ش��������⣺
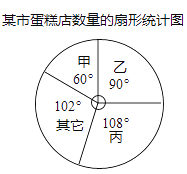
��1�����˾��Ӫ�ĵ�����������е�����������
��2����˾Ϊ�������г�ռ���ʣ������ڸ������走��������ﵽȫ�е�20%�����˾��Ҫ����ĵ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���֪��A![]() ����B
����B![]() ����C��y���ϵ�һ�����㣬����BCA��30��ʱ����C������Ϊ______��
����C��y���ϵ�һ�����㣬����BCA��30��ʱ����C������Ϊ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����⣺��ͼ1����Rt��ABC�У���C=90�㣬��ABC=30�㣬��D�DZ�CB������һ�㣬��ADE�ǵȱ������Σ��ҵ�E�ڡ�ACB���ڲ�������BE��̽���߶�BE��DE֮���������ϵ�������������̽�����̣��Ƚ�ͼ�����⻯���ó����룬�ٶ�һ��������з���������֤����
��1������D���C�غ�ʱ����ͼ2�������㲹ȫͼ�Σ��ɡ�BAC�Ķ���Ϊ ����E���� ______ �����ó�BE��DE֮���������Ϊ ��
��2������D��BC������һ�㣨�����B��C�غϣ�ʱ�����ͼ1��̽����1�����߶�BE��DE֮���������ϵ�Ƿ�������֤����Ľ��ۣ�
��3����ͼ3������PΪֱ��BC��һ�㣬����PABΪ���������Σ����������APB�Ķ���.
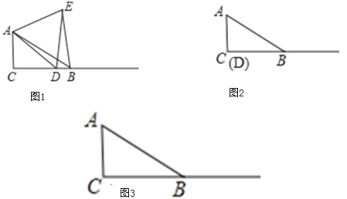
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ֽƬ�У�
ֽƬ�У�![]() ��
��![]() ��
��![]() ����
����![]() �ڱ�
�ڱ�![]() �ϣ���
�ϣ���![]() Ϊ�ۺ�
Ϊ�ۺ�![]() �۵��õ�
�۵��õ�![]() ��
��![]() ���
���![]() ���ڵ�
���ڵ�![]() ����
����![]() Ϊֱ�������Σ���
Ϊֱ�������Σ���![]() �ij���____��
�ij���____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲����и�ʽ
��x��1����x+1����x2��1
��x��1����x2+x+1����x3��1
��x��1����x3+x2+x+1����x4��1
��1���������Ϲ��ɣ���x��1����x6+x5+x4+x3+x2+x+1������ ����
��2�����ܷ��ɴ˹��ɳ�һ����ɣ�x��1����xn+xn��1+����+x+1������ ����
��3���������Ϲ�����32018+32017+32016+��32+3+1�Ľ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����Ϊ����3����6����������y=ax2+bx+c�����㣨��1����4���������н����д�����ǣ�������

A. b2��4ac
B. ax2+bx+c�ݩ�6
C. ���㣨��2��m��������5��n�����������ϣ���m��n
D. ����x��һԪ���η���ax2+bx+c=��4������Ϊ��5�ͩ�1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��AC�ֱ��ǰ���O��ֱ�����ң�OD��AC�ڵ�D������A������O������AP��AP��OD���ӳ��߽��ڵ�P������PC���ӳ���AB���ӳ��߽��ڵ�F��
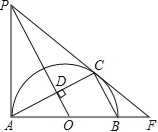
��1����֤��PC�ǰ���O�����ߣ�
��2������CAB=30����AB=10�����߶�BF�ij���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com