如图.点P是反比例函数的图象上的一点.小题1:求该反比例函数的解析式,小题2:设直线与双曲线的两个交点分别为P和P′.当＜时.直接写出x的取值范围．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

如图，点P（－3，1）是反比例函数

的图象上的一点.

小题1:求该反比例函数的解析式；
小题2:设直线

与双曲线

的两个交点分别为P和P′，
当

＜

时，直接写出x的取值范围．

小题1:∵点P（－3,1）在反比例函数

的图象上，
由

得

.
∴反比例函数的解析式为

.
小题1:

或

小题1:把A点坐标代入反比例函数解析式，即可求出m，确定出反比例解析式;
小题1:根据图像直接写出x的取值范围．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源：不详 题型：解答题

平安加气站某日的储气量为10000立方米．假设加气过程中每把加气枪均以每小时200立方米的速度为汽车加气．设加气站的储气量为y（立方米），加气总时间为x（小时）（加气期间关闭加气枪的时间忽略不计）．从7︰00开始，加气站加气枪的使用数量如下表所示：

时间段	7︰00—7︰30]	7︰30—8︰00	8︰00以后
加气枪使用︰数量（单位：把）	3	5	6

小题1:分别求出7︰00—7︰30及8︰00之后加气站的储气量y（立方米）与时间x（小时）的函数关系式．
小题2:若每辆车的加气量均为20立方米，请通过计算说明前50辆车能否在当天8︰00之前加完气．

查看答案和解析>>

科目：初中数学 来源：不详 题型：解答题

如图1，在平面直角坐标系中，点O是坐标原点，四边形ABCO是菱形，点A的坐标为（－3，4），点C在x轴的正半轴上，直线AC交y轴于点M，AB边交y轴于点H．

（1）求直线AC的解析式；
（2）连接BM，如图2，动点P从点A出发，沿折线ABC方向以2个单位／秒的速度向终点C匀速运动，设△PMB的面积为S（S≠0），点P的运动时间为t秒，求S与t之间的函数关系式（要求写出自变量t的取值范围）；
（3）在（2）的条件下，当 t为何值时，∠MPB与∠BCO互为余角．

查看答案和解析>>

科目：初中数学 来源：不详 题型：填空题

如图，在直角坐标系中，直线

分别与x轴、y轴交于点M、N，点A、B分别在y轴、x轴上，且∠B＝30°，AB＝4，将△ABO绕原点O顺时针转动一周，当AB与直线MN平行时点A的坐标为 ▲ .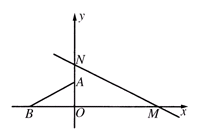

查看答案和解析>>

科目：初中数学 来源：不详 题型：解答题

某商店需要购进一批电视机和洗衣机，根据市场调查，决定电视机进货量不少于洗衣机进货量的一半．电视机与洗衣机的进价和售价如下表：

类别	电视机	洗衣机
进价(元/台)	1 800	1 500
售价(元/台)	2 000	1 600

计划购进电视机和洗衣机共 100 台，商店最多可筹集资金161 800 元．
(1)请你帮助商店算一算有多少种进货方案(不考虑除进价之外的其他费用)；
（2)哪种进货方案待商店销售购进的电视机与洗衣机完毕后获得的利润最多？并求出最大的利润(利润＝售价－进价)．

查看答案和解析>>

科目：初中数学 来源：不详 题型：解答题

我市水产养殖专业户王大爷承包了30亩水塘，分别养殖甲鱼和鳜鱼．有关成本和销售额见下表：

小题1:2011年，王大爷养殖甲鱼20亩，鳜鱼10亩．王大爷这一年共收益多少万元？（收益＝销售额－成本）
小题2:2011年，王大爷继续用这30亩水塘全部养殖甲鱼和鳜鱼，计划投入成本不超过70万元，若每亩养殖的成本、销售额与2011年相同，要获得最大收益，则他应养殖甲鱼和鳜鱼各多少亩？
小题3:已知甲鱼每亩需要饲料500 kg，鳜鱼每亩需要饲料700 kg．根据(2)中的养殖亩数，为了节约运输成本，实际使用的运输车辆每次装载饲料的总量是原计划每次装载总量的2倍，结果运输养殖所需全部饲料比原计划减少了2次，王大爷原定的运输车辆每次可装载多少饲料？

查看答案和解析>>

科目：初中数学 来源：不详 题型：单选题

若y＝x+2﹣3b是正比例函数，则b的值是（）．

A．0

B．