
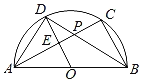
【题目】如图,AB是⊙O的直径,点C,点D是半圆上两点,连结AC,BD相交于点P,连结AD,OD.已知OD⊥AC于点E,AB=2.下列结论:
①AD2+BC2=4;
②sin∠DAC=![]() ;
;
③若AC=BD,则DE=OE;
④若点P为BD的中点,则DE=2OE.
其中正确的是( )

A.①②③B.②③④C.③④D.②④
【答案】B
【解析】
①错误.证明AC2+BC2=AB2=4即可判断.
②正确.证明∠DAC=∠CBP即可解决问题.
③正确.推出△AOD是等边三角形,即可解决问题.
④正确.利用全等三角形的性质证明DE=BC,再利用三角形的中位线定理证明BC=2OE即可解决问题.
解:∵AB是直径,
∴∠ACB=90°,
∴AC2+BD2=AB2=4,
∵AC>AD,
∴AD2+BC2<4,故①错误,
∵∠DAC=∠CBD,
∴sin∠DAC=sin∠CBD=![]() ,故②正确,
,故②正确,
∵AE⊥OE,
∴![]() =
=![]() ,
,
∵AC=BD,
∴![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
∴∠AOD=60°,
∵OA=OD,
∴△OAD是等边三角形,
∵AE⊥OD
∴DE=OE,故③正确,
∵∠DEP=∠BCP=90°,DP=PB,∠DPE=∠BPC,
∴△PDE≌△PBC(AAS),
∴DE=BC,
∵OE∥BC,AO=OB,
∴AE=EC,
∴BC=2OE,
∴DE=2OE,故④正确.
故选:B.


科目:初中数学 来源: 题型:
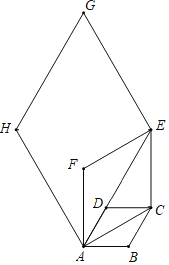
【题目】 如图,边长为1的菱形ABCD中,∠DAB=60°,连接AC,以AC为边在AC上方作第二个菱形ACEF,使∠FAC=60°.连接AE,再以AE为边在AE上方作第三个菱形AEGH,使∠HAE=60°.则菱形AEGH的周长为( )
A.![]() B.12C.3D.
B.12C.3D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2020年新冠肺炎疫情期间,我市某企业为支援湖北,准备将购买的70吨蔬菜运往武汉,现有甲、乙两种货车可以租用,已知2辆甲货车和3辆乙货车一次可运44吨蔬菜;3辆甲货车和1辆乙货车一次可运38吨蔬菜.
(1)求每辆甲种货车和每辆乙种货车一次分别能运多少吨蔬菜?
(2)已知甲种货车每辆租金500元,乙种货车每辆租金450元,该企业共租用甲、乙两种货车8辆,设租甲种货车a辆,求租车总费用w(元)与a之间的函数关系式,并求出自变量a的取值范围;
(3)在(2)的条件下,请你为该企业设计出费用最少的方案,并求出最少的租车费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,点D在AB上,以AD为直径的⊙O与边BC相切于点E,与边AC相交于点G,且![]() =
=![]() ,连接GO并延长交⊙O于点F,连接BF
,连接GO并延长交⊙O于点F,连接BF
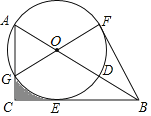
(1)求证:①AO=AG,②BF是⊙O的切线.
(2)若BD=6,求图形中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
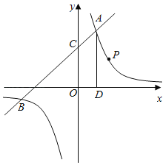
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() 和
和![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)![]() ,
,![]() ;
;
(2)根据函数图象知,
①当![]() 时,
时,![]() 的取值范围是 ;
的取值范围是 ;
②当![]() 为 时,
为 时,![]() .
.
(3)过点![]() 作
作![]() 轴于点
轴于点![]() ,点
,点![]() 是反比例函数在第一象限的图象上一点,设直线
是反比例函数在第一象限的图象上一点,设直线![]() 与线段
与线段![]() 交于点
交于点![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
(4)点![]() 是
是![]() 轴上的一个动点,当△MBC为直角三角形时,直接写出点
轴上的一个动点,当△MBC为直角三角形时,直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设一次函数y1=x+a+b和二次函数y2=x(x+a)+b.
(1)若y1,y2的图象都经过点(-2,1),求这两个函数的表达式;
(2)求证:y1,y2的图象必有交点;
(3)若a>0,y1,y2的图象交于点(x1,m),(x2,n)(x1<x2),设(x3,n)为y2图象上一点(x3≠x2),求x3-x1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
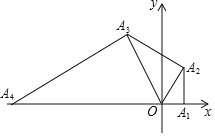
【题目】如图,在平面直角坐标系中,点A1的坐标为(1,0),以OA1为直角边作Rt△OA1A2,并使∠A1OA2=60°,再以OA2为直角边作Rt△OA2A3,并使∠A2OA3=60°,再以OA3为直角边作Rt△OA3A4,并使∠A3OA4=60°…按此规律进行下去,则点A2020的坐标为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了帮助本市一名患“白血病”的高中生,某班15名同学积极捐款,他们捐款数额如下表:
捐款的数额(单位:元) | 5 | 10 | 20 | 50 | 100 |
人数(单位:个) | 2 | 4 | 5 | 3 | 1 |
关于这15名同学所捐款的数额,下列说法正确的是
A.众数是100 B.平均数是30 C.极差是20 D.中位数是20
查看答案和解析>>
科目:初中数学 来源: 题型:
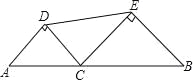
【题目】如图,线段 AB 的长为 4,C 为 AB 上一个动点,分别以 AC、BC 为斜边在 AB 的同侧作两个等腰直角三角形 ACD 和 BCE, 连结 DE, 则 DE 长的最小值是( )
A. ![]() B. 2C.
B. 2C. ![]() D. 4
D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com