
分析 利用平行四边形的性质和角平分线证出∠DAE=∠BEA,得出AB=BE,由此求出另一边,从而求出周长,注意两种情况.
解答 解:如图所示: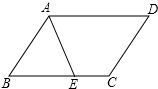
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,AD∥BC,
∵∠A的平分线交BC于点E,
∴∠BAE=∠DAE
∵AD∥BC,
∴∠DEA=∠BEA,
∴∠DAE=∠BEA
∴AB=BE,
分两种情况进行讨论:
当BE=3cm,EC=4cm时,AB=BE=3cm,BC=7cm,平行四边形的周长=2(3+7)=20(cm);
当BE=4cm,EC=3cm时,AB=BE=4cm,BC=7cm,平行四边形的周长=2(4+7)=22(cm);
综上所述:?ABCD的周长是22或22cm.
故答案为20或22.
点评 本题考查了平行四边形的性质、等腰三角形的判定;熟练掌握平行四边形的性质,证明AB=BE是解题的关键.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:解答题
 甲、乙两人分别骑自行车和摩托车沿相同路线由A地到相距80千米的B地,行驶过程中的函数图象如图所示.
甲、乙两人分别骑自行车和摩托车沿相同路线由A地到相距80千米的B地,行驶过程中的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
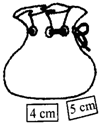 如图所示,口袋中有5张完全相同的卡片,分别写有1cm,2cm,3cm,4cm和5cm,口袋外有两张卡片,分别写有4cm和5cm.现随机从袋内取出一张卡片,与口袋外两张卡片放在一起,以卡片上的数量分别作为三条线段的长度,按要求回答下列问题:
如图所示,口袋中有5张完全相同的卡片,分别写有1cm,2cm,3cm,4cm和5cm,口袋外有两张卡片,分别写有4cm和5cm.现随机从袋内取出一张卡片,与口袋外两张卡片放在一起,以卡片上的数量分别作为三条线段的长度,按要求回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 1号 | 2号 | 3号 | 4号 | 5号 | 总个数 | |
| 甲班 | 89 | 100 | 98 | 110 | 103 | 500 |
| 乙班 | 100 | 89 | 97 | 119 | 95 | 500 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com