
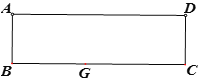
【题目】如图,在矩形纸片ABCD中,AB=4,点G是BC边上一点,且BG=5(BG<CG). 将矩形纸片沿过点G的折痕GE折叠,使点B恰好落在AD边上,折痕与矩形纸片ABCD的边相交于点E,则折痕GE的长为_______.
【答案】![]() 或
或![]()
【解析】
分两种情况讨论:①当点E在AB边上时,那么结合折叠的性质及已知条件可得AH=BG=FG=5,GH=AB=4,进而在Rt△FHG中运用勾股定理易得FH=3,则AF =2;设EF=BE=x,列方程可求出EF,然后可求出EG;②当点E在AD边上时,结合折叠的性质可得BG=FG=5,HF=AB=EK=4,易得∠BGE=∠EGF,结合AD∥BC,进而可得∠FEG=∠BGE=∠EGF,则BE=EF=FG=5,然后根据BK2=BE2-EK2可求得BK,至此再根据EG2=EK2+KG2=20解答即可.
解:
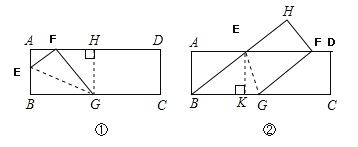
如图①:当点E在AB边上时,根据已知可得AH=BG=FG=5,GH=AB=4.
∵FG=5,GH=4,
∴FH=3,
∴AF=AH-FH=2.
设EF=BE=x,则AE=4-x,
∴(4-x)2+22=x2,
∴x=![]() ,
,
∴EF2+FG2=EG2,
∴(![]() )2+52=EG2,
)2+52=EG2,
∴EG=![]() .
.
如图②:当点E在AD边上时,可得BG=FG=5,HF=AB=EK=4.
∵EG为折痕,
∴∠BGE=∠EGF.
∵AD∥BC,
∴∠FEG=∠BGE=∠EGF,
∴BE=EF=FG=5,
∴BK2=BE2-EK2,
∴BK=3,
∴KG=2,
∴EG2=EK2+KG2=20,
∴EG=![]() .
.
综上EG的长为![]() 或
或![]() .
.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
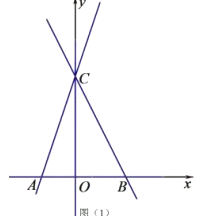
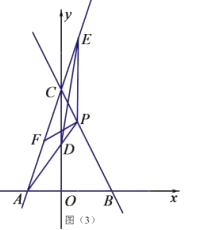
【题目】如图,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,且
,且![]() .
.
![]() 求直线
求直线![]() 的解析式;
的解析式;
![]() 点
点![]() 在线段
在线段![]() 上,连接
上,连接![]() 交
交![]() 轴于点,过点
轴于点,过点![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,设点
,设点![]() 的坐标为
的坐标为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式(不要求写自变量的取值范围).
的函数关系式(不要求写自变量的取值范围).
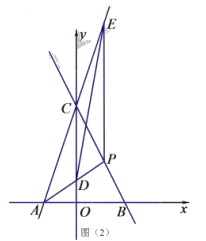
![]() 在
在![]() 的条件下,点
的条件下,点![]() 是线段
是线段![]() 上一点,连接
上一点,连接![]() ,当
,当![]() 时,且
时,且![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中装有![]() 个小球,它们除了颜色不同外,其余都相同, 其中有 5 个白球,每次试验前,将盒子中的小球摇匀,随机摸出一个球记下颜色后再放回盒中.下表是摸球试验的一组统计数据:
个小球,它们除了颜色不同外,其余都相同, 其中有 5 个白球,每次试验前,将盒子中的小球摇匀,随机摸出一个球记下颜色后再放回盒中.下表是摸球试验的一组统计数据:
摸球次数( n ) | 50 | 100 | 150 | 200 | 250 | 300 | 500 |
摸到白球次( m ) | 28 | 60 | 78 | 104 | 123 | 152 | 251 |
白球频率( | 0.56 | 0.60 | 0.52 | 0.52 | 0.49 | 0.51 | 0.50 |
由上表可以推算出a大约是( )
A.10B.14C.16D.40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,过点
中,过点![]() 的直线交
的直线交![]() 轴正半轴于点
轴正半轴于点![]() ,将直线
,将直线![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() 后,分别与
后,分别与![]() 轴
轴![]() 轴交于点
轴交于点![]() 、
、![]() .
.
(1)若![]() ,求直线
,求直线![]() 的函数关系式;
的函数关系式;
(2)连接![]() ,若
,若![]() 的面积是5,求点
的面积是5,求点![]() 的运动路径长.
的运动路径长.

查看答案和解析>>
科目:初中数学 来源: 题型:
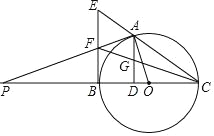
【题目】如图,点A是以BC为直径的⊙O上一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,G是AD的中点,连接CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P,且FG=FB=3.
(1)求证:BF=EF;
(2)求tanP;
(3)求⊙O的半径r.
查看答案和解析>>
科目:初中数学 来源: 题型:
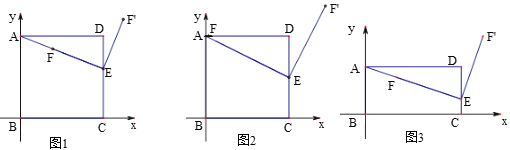
【题目】正方形ABCD的边长为4,以B为原点建立如图1平面直角坐标系中,E是边CD上的一个动点,F是线段AE上一点,将线段EF绕点E顺时针旋转90°得到EF'.
(1)如图2,当E是CD中点,![]() 时,求点F'的坐标.
时,求点F'的坐标.
(2)如图1,若![]() ,且F',D,B在同一直线上时,求DE的长.
,且F',D,B在同一直线上时,求DE的长.
(3)如图3,将正边形ABCD改为矩形,AD=4,AB=2,其他条件不变,若![]() ,且F',D,B在同一直线上时,则DE的长是_______.(请用含n的代数式表示)
,且F',D,B在同一直线上时,则DE的长是_______.(请用含n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题10分)如图,AB是半圆O的直径,CD⊥AB于点C,交半圆于点E, DF切半圆于点F。已知∠AEF=135°。
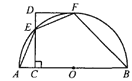
(1)求证:DF∥AB;
(2)若OC=CE,BF=![]() ,求DE的长。
,求DE的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
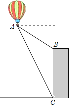
【题目】如图,热气球的探测器显示,从热气球A看一栋大楼顶部B的俯角为![]() ,看这栋大楼底部C的俯角为
,看这栋大楼底部C的俯角为![]() ,热气球A的高度为270米,则这栋大楼的高度为______米
,热气球A的高度为270米,则这栋大楼的高度为______米![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
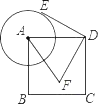
【题目】如图,已知正方形ABCD的边长为2,以点A为圆心,1为半径作圆,E是⊙A上的任意一点,将点E绕点D按逆时针方向旋转90°得到点F,则线段AF的长的最小值_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com