
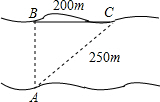
 如图,小红欲横渡一条河,由于水流的影响,实际上岸地点C偏离欲到达点B200m,结果他在水中实际游了250m,则该河流的宽度为
如图,小红欲横渡一条河,由于水流的影响,实际上岸地点C偏离欲到达点B200m,结果他在水中实际游了250m,则该河流的宽度为科目:初中数学 来源: 题型:
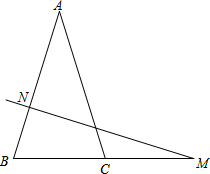 如图,在△ABC中,AB=AC,N是AB上任一点(不与A、B重合),过N作NM⊥AB交BC所在直线于M,
如图,在△ABC中,AB=AC,N是AB上任一点(不与A、B重合),过N作NM⊥AB交BC所在直线于M,查看答案和解析>>
科目:初中数学 来源: 题型:
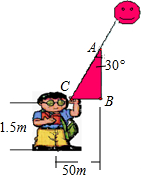 小刚家住在高层公寓的24楼,他很想知道他家离地面到底有多高.为此他在地面上进行了如图所示的测量.其中A点是小刚家,小刚身高1米五,BC距离50米.你能通过小刚的办法计算出小刚家距地面有多高吗?(请用含有根号的式子表示)
小刚家住在高层公寓的24楼,他很想知道他家离地面到底有多高.为此他在地面上进行了如图所示的测量.其中A点是小刚家,小刚身高1米五,BC距离50米.你能通过小刚的办法计算出小刚家距地面有多高吗?(请用含有根号的式子表示)查看答案和解析>>
科目:初中数学 来源: 题型:
| A、4x2-5x+4 |
| B、10x2-5x+4 |
| C、4x2+7x-6 |
| D、-4x2-7x+6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com