
如图,点M是反比例函数y= 在第一象限内图象上的点,作MB⊥x轴于B.过点M的第一条直线交y轴于点A1,交反比例函数图象于点C1,且A1C1=
在第一象限内图象上的点,作MB⊥x轴于B.过点M的第一条直线交y轴于点A1,交反比例函数图象于点C1,且A1C1=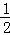 A1M,△A1C1B的面积记为S1;过点M的第二条直线交y轴于点A2,交反比例函数图象于点C2,且A2C2=
A1M,△A1C1B的面积记为S1;过点M的第二条直线交y轴于点A2,交反比例函数图象于点C2,且A2C2= A2M,△A2C2B的面积记为S2;过点M的第三条直线交y轴于点A3,交反比例函数图象于点C3,且A3C3=
A2M,△A2C2B的面积记为S2;过点M的第三条直线交y轴于点A3,交反比例函数图象于点C3,且A3C3= A3M,△A3C3B的面积记为S3;以此类推…;则S1+S2+S3+…+S8= _________ .
A3M,△A3C3B的面积记为S3;以此类推…;则S1+S2+S3+…+S8= _________ .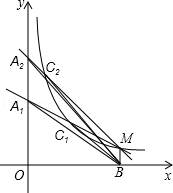
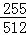
解析试题分析:根据点M是反比例函数y= 在第一象限内图象上的点,即可得出
在第一象限内图象上的点,即可得出 =
= OB×MB=
OB×MB= ,再利用C1到BM的距离为A1到BM的距离的一半,得出S1=
,再利用C1到BM的距离为A1到BM的距离的一半,得出S1=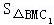 =
=
 =
= ,同理即可得出S2=
,同理即可得出S2=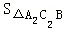 =
=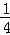
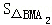 =
=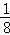 ,S3=
,S3=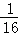 ,S4=
,S4=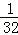 …,进而求出S1+S2+S3+…+S8的值即可.
…,进而求出S1+S2+S3+…+S8的值即可.
过点M作MD⊥y轴于点D,过点A1作A1E⊥BM于点E,过点C1作C1F⊥BM于点F,
∵点M是反比例函数y= 在第一象限内图象上的点,
在第一象限内图象上的点,
∴OB×BM=1,
∴ =
= OB×MB=
OB×MB= ,
,
∵A1C1= A1M,即C1为A1M中点,
A1M,即C1为A1M中点,
∴C1到BM的距离C1F为A1到BM的距离A1E的一半,
∴S1=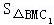 =
=
 =
= ,
,
∴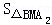 =
= BM•A2到BM距离=
BM•A2到BM距离= ×BM×BO=
×BM×BO= ,
,
∵A2C2=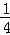 A2M,
A2M,
∴C2到BM的距离为A2到BM的距离的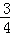 ,
,
∴S2=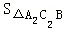 =
=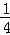
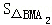 =
=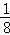 ,
,
同理可得:S3=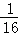 ,S4=
,S4=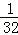 …
…
∴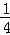 +
+ +…+
+…+ +
+ ,=
,= +
+ +…+
+…+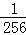 +
+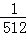 =
=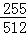 .
.
考点:反比例函数的综合应用,三角形面积关系
点评:根据同底三角形对应高的关系得出面积关系是解题关键.


科目:初中数学 来源: 题型:
| k |
| x |
| k |
| x |
| k |
| x |

查看答案和解析>>
科目:初中数学 来源:2010-2011学年湖北省枝江市初三下学期第一次单元测试数学卷 题型:选择题
如图,点P(3a,a)是反比例函y=(k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为( )

A.y= B.y= C.y= D.y=
查看答案和解析>>
科目:初中数学 来源:2013届湖北省枝江市初一上学期第一次单元检测数学卷 题型:选择题
如图,点P(3a,a)是反比例函y=(k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为( )

A.y= B.y= C.y= D.y=
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com