
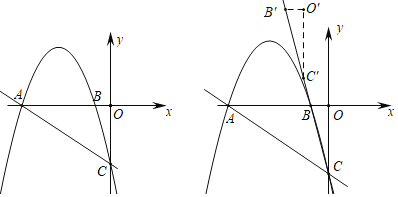
【题目】如图1,在平面直角坐标系中,抛物线y=﹣![]() x2﹣
x2﹣![]() x﹣3交x轴于A,B两点(点A在点B的左侧),交y轴于点C
x﹣3交x轴于A,B两点(点A在点B的左侧),交y轴于点C
(1)求直线AC的解析式;
(2)点P是直线AC上方抛物线上的一动点(不与点A,点C重合),过点P作PD⊥x轴交AC于点D,求PD的最大值;
(3)将△BOC沿直线BC平移,点B平移后的对应点为点B′,点O平移后的对应点为点O′,点C平移后的对应点为点C′,点S是坐标平面内一点,若以A,C,O′,S为顶点的四边形是菱形,求出所有符合条件的点S的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)(
;(3)(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() )或(
)或(![]() )或(
)或(![]() )
)
【解析】
(1)![]() ,令y=0,则x=-1或-6,故点A、B、C的坐标分别为:(-6,0)、(-1,0)、(0,-3),然后用待定系数法即可求解;(2)设点P(x,
,令y=0,则x=-1或-6,故点A、B、C的坐标分别为:(-6,0)、(-1,0)、(0,-3),然后用待定系数法即可求解;(2)设点P(x,![]() ),则点D(x,
),则点D(x,![]() ),则PD=
),则PD=![]() -(
-(![]() )=
)=![]() ,然后配方法分析其最值,即可求解;(3)分AC是菱形的边、AC是对角线两种情况,分别求解即可.
,然后配方法分析其最值,即可求解;(3)分AC是菱形的边、AC是对角线两种情况,分别求解即可.
解:(1)当y=0时,![]()
解得:x=-1或-6,
当x=0时,y=-3
∴点A、B、C的坐标分别为:(-6,0)、(-1,0)、(0,-3),
设直线AC的表达式为:![]()
将点A、C的坐标代入得:![]()
解得: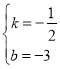
∴直线AC的解析式为:![]()
(2)设点P(x,![]() ),则点D(x,
),则点D(x,![]() )
)
则PD=![]() -(
-(![]() )=
)=![]()
∵![]() <0,故PD有最大值为
<0,故PD有最大值为![]()
(3)设直线BC的表达式为:![]()
将点B、C的坐标代入得:![]()
解得:![]()
∴直线BC的解析式为:![]()
①如图3或4中,当四边形ACSO'是菱形时,设AS交CO′于K,AC=AO′=3![]() ,
,
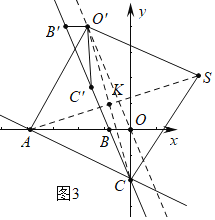
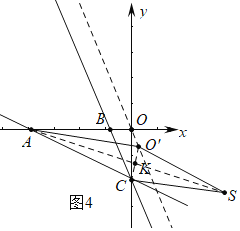
点O平移后的对应点为点O′,平移直线的k为![]() ,
,
则设点O向左平移m个单位,则向上平移3m个单位,则点O′(-m,3m),设点S(a,b),
∴(m+6)2+(-3m)2=(3![]() )2,
)2,
解得m=![]() ,
,
∴O′(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)
由中点公式可得:K(![]() ,
,![]() )或(
)或(![]() ,
,),
∵AK=KS,
∴S(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)
②如图5或6中,当四边形ACO'S是菱形时,设CS交AO′于K,AC=CO′=3![]() ,
,
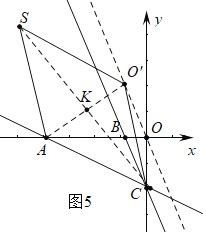
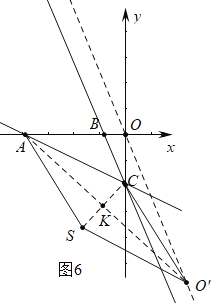
∵点O平移后的对应点为点O′,平移直线的k为![]() ,C(0,-3),设O′(m,-3m),
,C(0,-3),设O′(m,-3m),
∴m2+(-3m+3)2=(3![]() )2,
)2,
解得m=![]() ,
,
∴O′(![]() )或(
)或(![]() ),
),
由中点公式可得:K(![]() )或(
)或(![]() ),
),
∵CK=KS,
∴S(![]() )或(
)或(![]() )
)
③如图7中,当四边形ASCO′是菱形时,SO垂直平分线段AC,
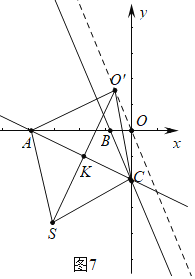
直线SO′的解析式为![]()
由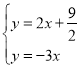 ,
,
解得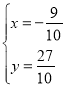 ,
,
∴O′(![]() )
)
∵KS=KO′,
∴S(![]() )
)
综上所述,满足条件的点S坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() )或(
)或(![]() )或(
)或(![]() )
)


科目:初中数学 来源: 题型:
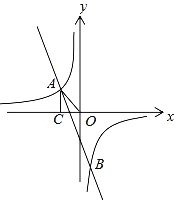
【题目】如图,一次函数y=kx+b的图象与反比例函数![]() 的图象相交于A(m,4)、B(2,﹣6)两点,过A作AC⊥x轴交于点C,连接OA.
的图象相交于A(m,4)、B(2,﹣6)两点,过A作AC⊥x轴交于点C,连接OA.
(1)分别求出一次函数与反比例函数的表达式;
(2)若直线AB上有一点M,连接MC,且满足S△AMC=3S△AOC,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
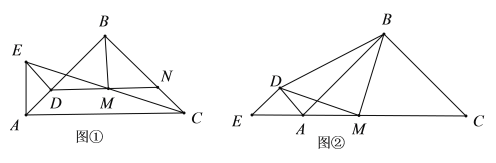
【题目】如图①,已知点![]() 在线段
在线段![]() 上,在
上,在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,
![]() ,且
,且![]() 为
为![]() 的中点.
的中点.
(1)连接![]() 并延长交
并延长交![]() 于
于![]() ,求证:
,求证:![]() ;
;
(2)直接写出线段![]() 与
与![]() 的关系: ;
的关系: ;
(3)若将![]() 绕点
绕点![]() 逆时针旋转,使点
逆时针旋转,使点![]() 在线段
在线段![]() 的延长线上(如图②所示位置),则(2)中的结论是否仍成立?若成立,请证明;若不成立,请说明理由.
的延长线上(如图②所示位置),则(2)中的结论是否仍成立?若成立,请证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 的图像与x轴交于A、B两点,与y轴交于点C,其顶点为P,连接PA、AC、CP,过点C作y轴的垂线l.已知顶点P的坐标为(-3,-4),线段PC之长为3
的图像与x轴交于A、B两点,与y轴交于点C,其顶点为P,连接PA、AC、CP,过点C作y轴的垂线l.已知顶点P的坐标为(-3,-4),线段PC之长为3![]()
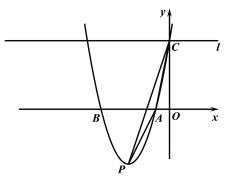
(1)求二次函数解析式。
(2)M为直线l上一点,且以M,C,O为顶点的三角形与以A,C,O为顶点的三角形相似,请直接写出点M的坐标。
(3)直线l上是否存在点D,使△PBD的面积等于△PAC的面积的3倍?若存在,求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y=![]() 的图象与一次函数y=kx+b的图象交于A,B两点,
的图象与一次函数y=kx+b的图象交于A,B两点,
点A的坐标为(2,6),点B的坐标为(n,1).
(1)求反比例函数与一次函数的表达式;
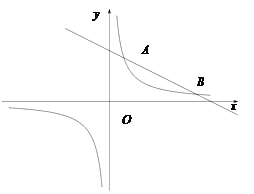
(2)点E为y轴上一个动点,若S△AEB=10,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
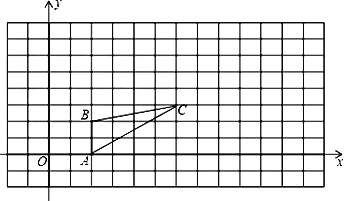
【题目】如图,图中的小方格都是边长为1的正方形,△ABC的A、B、C三点坐标为A(2,0)、B(2,2)、C(6,3)。
(1) 请在图中画出一个△![]() ,使△
,使△![]() 与△ABC是以坐标原点为位似中心,相似比为2的位似图形。
与△ABC是以坐标原点为位似中心,相似比为2的位似图形。
(2)求△![]() 的面积。
的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里装有4个大小、质地均相同的乒乓球,每个球上面分别标有1,2,3,4.小林先从布袋中随机抽取一个乒乓球(不放回去),再从剩下的3个球中随机抽取第二个乒乓球.
(1)请你用树状图或列表法列出所有可能的结果;
(2)求两次取得乒乓球的数字之积为奇数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
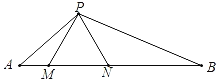
【题目】如图,在△PAB中,M.N是AB上两点,△PMN是等边三角形,∠APM=∠B.
(1)求证:∠A=∠BPN;
(2)求证:MN2=AM·BN;
(3)若AP=![]() ,AM=1,求线段MN,PB的长.
,AM=1,求线段MN,PB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com