
分析 (1)根据有理数的乘方,有理数的乘法以及有理数的加法运算法则进行计算即可得解;
(2)先根据除以一个数等于乘以这个数的倒数转化为乘法,有理数的乘方和乘法运算法则计算,再利用乘法分配律进行计算即可得解;
(3)根据有理数的乘方和除法运算法则,乘法分配律进行计算即可得解;
(4)根据有理数的乘方,绝对值的性质,有理数的除法以及立方根的定义进行计算即可得解.
解答 解:(1)3×(-1)3+(-5)×(-3),
=3×(-1)+15,
=-3+15,
=12;
(2)($\frac{1}{2}$-$\frac{1}{3}$)÷(-$\frac{1}{6}$)+(-2)2×(-14),
=($\frac{1}{2}$-$\frac{1}{3}$)×(-6)+4×(-14),
=$\frac{1}{2}$×(-6)-$\frac{1}{3}$×(-6)-56,
=-3+2-56,
=-59+2,
=-57;
(3))(-3)2÷3+($\frac{1}{2}$-$\frac{2}{3}$)×12-(-1)2012,
=9÷3+$\frac{1}{2}$×12-$\frac{2}{3}$×12-1,
=3+6-8-1,
=9-9,
=0;
(4)-24-|-5|+6÷(-$\frac{2}{3}$)×$\root{3}{-8}$,
=-16-5+6×(-$\frac{3}{2}$)×(-2),
=-16-5+18,
=-21+18,
=-3.
点评 本题主要考查了实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握有理数的乘方,有理数的加法,有理数的减法、二次根式、绝对值等考点的运算.


科目:初中数学 来源: 题型:填空题
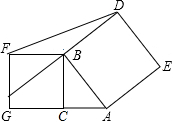 如图所示,在Rt△ABC中,∠ACB=90°,以AB、BC为边向外作正方形ABDE、BCGF,连接DF,且S正方形ABDE=7,S正方形BCGF=3,则△DBF的面积等于$\sqrt{3}$.
如图所示,在Rt△ABC中,∠ACB=90°,以AB、BC为边向外作正方形ABDE、BCGF,连接DF,且S正方形ABDE=7,S正方形BCGF=3,则△DBF的面积等于$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
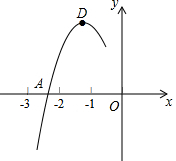 抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:①b2-4ac<0;②a+b+c<0;③c-a=2;④方程ax2+bx+c-2=0有两个相等的实数根,其中正确结论的个数为3个.
抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:①b2-4ac<0;②a+b+c<0;③c-a=2;④方程ax2+bx+c-2=0有两个相等的实数根,其中正确结论的个数为3个.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
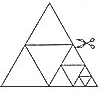 如图,将一张等边三角形纸片沿任意两边中点的连线可剪成4个小三角形,称为第一次操作;然后,将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作:…,根据以上操作,若操作的次数是n时,则可得到的小三角形个数为( )
如图,将一张等边三角形纸片沿任意两边中点的连线可剪成4个小三角形,称为第一次操作;然后,将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作:…,根据以上操作,若操作的次数是n时,则可得到的小三角形个数为( )| A. | 3n-1 | B. | 3(n-1) | C. | 3(n+1) | D. | 3n+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6x-1=1 | B. | 7x-1=x+1 | C. | 2x=$\frac{2}{3}$ | D. | 5x-x=2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com