
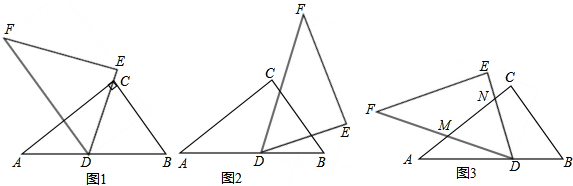
分析 (1)先判定三角形ACD是等腰三角形,再判定DG⊥AC,最后根据三线合一求得GC的长;
(2)先连接CD,再判定△DNC∽△MDB,最后根据相似三角形对应边成比例,列出比例式并变形,即可得到函数关系式以及定义域;
(3)根据△DMN是等腰三角形,需要分三种情况进行讨论,分别求得AN的长即可.
解答 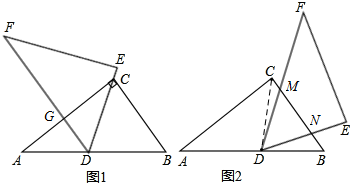 解:(1)如图1,∵△ABC≌△FDE,
解:(1)如图1,∵△ABC≌△FDE,
∴∠GDC=∠B,
∵点D是边AB的中点,
∴CD=AD=BD=$\frac{1}{2}$AB,
∴∠DCB=∠B,
∴∠GDC=∠DCB,
∴BC∥DG,
∴∠AGD=∠ACB=90°,
∵AD=CD,
∴GC=$\frac{1}{2}$AC=4;
(2)如图2,连接CD,
在直角三角形ABC中,由勾股定理可得AB=10,
∵点D为AB的中点,∠ACB=90°,
∴BD=CD=$\frac{1}{2}$AB=5,
∴∠B=∠DCN,①
∵∠CND=∠B+∠BDN,∠BDM=∠MDN+∠BDN,且∠B=∠MDN,
∴∠CND=∠BDM,②
由①②可得△DNC∽△MDB,
∴$\frac{CD}{BM}$=$\frac{CN}{BD}$,即$\frac{5}{y}$=$\frac{x}{5}$,
∴$y=\frac{25}{x}$,
∵DF、DE分别交线段BC于点M、N,
∴CN≤CB,BM≤BC,
∴x≤6,y≤6即$\frac{25}{x}$≤6,
解得$\frac{25}{6}$≤x≤6;
(3)△DMN是等腰三角形,分三种情况:
①如图3,当DM=MN时,∠MND=∠MDN=∠B,
由∠B+∠A=90°,可得∠DNM+∠A=90°,即ND⊥AD,
∴∠ADN=∠C=90°,
又∵∠A=∠A,
∴△ADN∽△ACB,
∴$\frac{DN}{CB}$=$\frac{AD}{AC}$,即$\frac{DN}{6}$=$\frac{5}{8}$,
∴DN=$\frac{15}{4}$,
∴直角三角形ADN中,AN=$\sqrt{{5}^{2}+(\frac{15}{4})^{2}}$=$\frac{25}{4}$,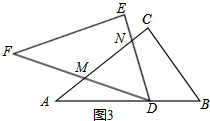
②如图4,当NM=ND时,∠DMH=∠MDN=∠B,
过D作DH⊥MN于H,则∠DHM=∠C=90°,DH=$\frac{1}{2}$BC=3,
∴△DHM∽△ACB,
∴$\frac{MH}{BC}$=$\frac{DH}{AC}$,即$\frac{MH}{6}$=$\frac{3}{8}$,
∴MH=$\frac{9}{4}$,
∴DN=MN=$\frac{9}{4}$+HN,
∴直角三角形DHN中,HN2+HD2=DN2,即HN2+32=($\frac{9}{4}$+HN)2,
解得HN=$\frac{7}{8}$,
又∵直角三角形ADH中,AH=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴AN=AH+HN=4+$\frac{7}{8}$=$\frac{39}{8}$,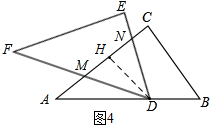
③如图5,当DN=DM时,设DN=DM=y,MN=2x,
过D作DH⊥MN于H,则MH=NH=$\frac{1}{2}$MN=x,
过N作NQ⊥MD于Q,则∠NQD=∠C=90°,
∵∠NDQ=∠B,
∴△NDQ∽△ABC,
∴$\frac{ND}{AB}$=$\frac{NQ}{AC}$,即$\frac{y}{10}$=$\frac{NQ}{8}$,
∴NQ=$\frac{4}{5}$y,
∵$\frac{1}{2}$×MN×DH=$\frac{1}{2}$×DM×NQ,
∴2x×3=y×$\frac{4}{5}$y,即y2=$\frac{30}{4}$x,
又∵直角三角形DHN中,DN2=DH2+HN2,即y2=32+x2
∴$\frac{30}{4}$x=32+x2
解得x1=1.5,x2=6(舍去),
∴HN=1.5
又∵直角三角形ADH中,AH=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴AN=AH+HN=4+1.5=$\frac{11}{2}$,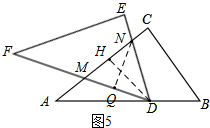
故AN的值为:$\frac{25}{4}$或$\frac{39}{8}$或$\frac{11}{2}$.
点评 本题以旋转变换为背景,考查了等腰三角形的性质以及相似三角形的判定与性质.在解决等腰三角形的问题时,一般需要作辅助线,运用三线合一的性质进行求解,有时需要进行分类讨论,分类时要注意不能遗漏,不能重复.


科目:初中数学 来源: 题型:选择题
| A. | 等腰三角形 | B. | 直角三角形 | C. | 等腰直角三角形 | D. | 钝角三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
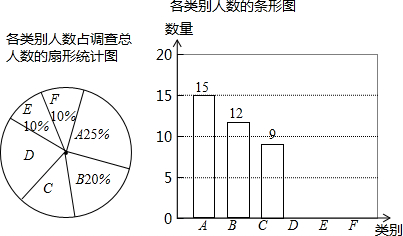
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
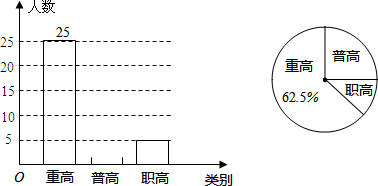
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
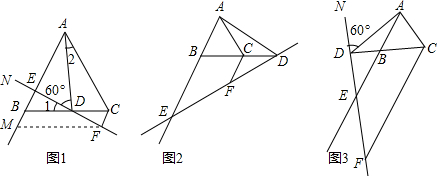
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com