
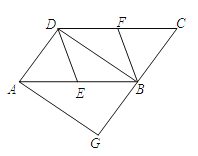
����Ŀ���ڡ�ABC�У�BC��6��S��ABC��18��������DEFG�ı�FG��BC�ϣ�����D��E�ֱ���AB��AC�ϣ�
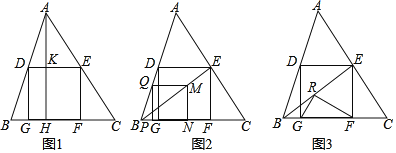
��1����ͼ1������A��AH��BC�ڵ�H����DE�ڵ�K����������DEFG�ı߳���
��2����ͼ2����BE��ȡ��M����MN��BC�ڵ�N��MQ��DE��AB�ڵ�Q��QP��BC�ڵ�P����֤���ı���MNPQ�������Σ�
��3����ͼ3����BE��ȡ��R��ʹRE��FE������RG��RF����tan��EBF��![]() ����֤����GRF��90����
����֤����GRF��90����
���𰸡���1��3����2������������3��������
��������
��1����ͼ1�У���������DEFG�ı߳�Ϊx���������������εĶ�Ӧ�ߵıȵ������Ʊȹ������̼��ɽ�����⣮
��2������ƽ���߷��߶γɱ�������֤��MN��MQ����֤���ı���MNPQ��ƽ���ı��μ��ɽ�����⣮
��3����EF��GF��3k��BF��4k����BG��k��BE��5k���ɵ�BR2��BGBF��4k2���Ƴ�![]() ���Ƴ���RBG�ס�FBR���Ƴ���BRG����RFB����֤����ERF+��BRG��90���ɵý��ۣ�
���Ƴ���RBG�ס�FBR���Ƴ���BRG����RFB����֤����ERF+��BRG��90���ɵý��ۣ�
�⣺��1����ͼ1�У���������DEFG�ı߳�Ϊx��
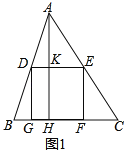
��AH��BC��
��S��ABC��![]() BCAH��18��
BCAH��18��
��![]() ��6��AH��18��
��6��AH��18��
��AH��6��
���ı���DEFG�������Σ�
��DE��BC��
���ADE�ס�ABC��
��![]() ��
��
��![]() ��
��
��x��3��
��������DEFG�ı߳�Ϊ3��
��2��֤������ͼ2�У�

��MN��BC���ı���DEFG�������Σ�
���MNB����EFB��90����DE��EF��
��MN��EF��
��![]() ��
��
��MQ��DE��
��![]() ��
��
��![]() ��
��
��MN��MQ��
��QP��BC��MN��BC��
��QP��MN��
��MQ��DE��DE��BC��
��QM��PN��
���ı���MNPQ��ƽ���ı��Σ�
�ߡ�MNP��90����
���ı���MNPQ�Ǿ��Σ�
��MN��MQ��
���ı���MNPQ�������Σ�
��3��֤������ͼ3�У�
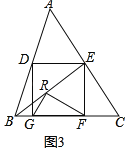
��Rt��EBF����tan��EBF��![]() ��
��
����Լ���EF��GF��3k��BF��4k����BG��k��BE��5k��
��ER��EF��3k��
��BR��BE��ER��2k��
��BR2��BGBF��4k2��
��![]() ��
��
�ߡ�RBG����RBF��
���RBG�ס�FBR��
���BRG����RFB��
��ER��EF��
���ERF����EFR��
�ߡ�EFR+��BFR��90����
���ERF+��BRG��90����
���FRG��90����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
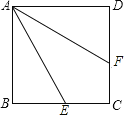
����Ŀ����ͼ���ı���ABCD�������Σ���E��F�ֱ����߶�BC��DC�ϣ��߶�AE�Ƶ�A��ʱ����ת�����߶�AF�غϣ���![]() ������ת�ĽǶ��ǣ� ��
������ת�ĽǶ��ǣ� ��
A.![]() B.
B.![]()
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����![]() �У�
�У�![]() �ֱ��ڱ�
�ֱ��ڱ�![]() ���е㣬
���е㣬![]() �ǶԽ��ߣ�����
�ǶԽ��ߣ�����![]() ��
��![]() ����
����![]() ���ӳ�����
���ӳ�����![]() ��
��
��1����֤���ı���![]() ��ƽ���ı��Σ�
��ƽ���ı��Σ�
��2�����ı���![]() �Ǿ��Σ����ı���
�Ǿ��Σ����ı���![]() ��ʲô�����ı��Σ���֤����Ľ��ۣ�
��ʲô�����ı��Σ���֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڰ�ԲO�У�ABΪֱ����AC��ADΪ�����ң��ҡ�CAD+��CAB��90�㣮
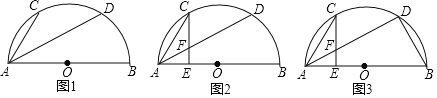
��1����ͼ1����֤����AC���ڻ�CD��
��2����ͼ2����E��ֱ��AB�ϣ�CE��AD�ڵ�F����AF��CF����֤��AD��2CE��
��3����ͼ3���ڣ�2���������£�����BD����AE��4��BD��12������AC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����ʵ����ƶ��С���ĺ�ΰĿ�꣬���н�ϱ��طḻ��ɽˮ��Դ��������չ����ҵ������ׯ�ڵ���������֧���£��������������磬ר�ŽӴ��οͣ������繲��80��ͷ������ݺ������ṩ�ķ��䵥��x��Ԫ�����ο;�ס������y���䣩����Ϣ�����ֻ��Ƴ�y��x�ĺ���ͼ����ͼ��ʾ��
��1����y��x֮��ĺ�����ϵʽ��
��2��������涨ÿ������۸���60Ԫ�Ҳ�����150Ԫ�������ο�����ס��ÿ�����䣬������ÿ����֧��20Ԫ�ĸ��ַ��ã����۶�Ϊ����ʱ��������ÿ����������������Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
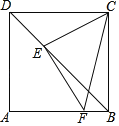
����Ŀ����ͼ����������ABCD�У�AB��6����E�ڶԽ���BD�ϣ�DE��2![]() ������CE������E��EF��CE�����߶�AB�ڵ�F
������CE������E��EF��CE�����߶�AB�ڵ�F
��1����֤��CE��EF��
��2����FB�ij���
��3������FC��BD�ڵ�G����BG�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ϊ���˽�괺��ʱѧ���ĸ������������������һ��ѧУ�ij����꼶�������ȡ�˲���ѧ����������������е��飬�����ⲿ��ѧ�������Ѷ���Ƴ�Ƶ�ʷֲ�ֱ��ͼ����֪�������ҵ�һ�������Ϊ12�����������������Ϣ�ش�

��1������ȡ�����ѧ������Ϊ ����
��2���������ҵ������Ƶ���� ��
��3������ÿ���ƽ�����Ѷ��Ը������Сֵ���㣬��ô����ȡѧ�����ε����ƽ�����Ѷ�Ϊ Ԫ��
��4���Եڣ�3��С������õ����ƽ�����Ѷ������Ƹõ���ȫ��ѧ�����ε����ƽ�����Ѷ����Ϊ�Ƿ��������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�����������y![]() ��ͼ����P��3��4����
��ͼ����P��3��4����
��1����k��ֵ��
��2����OP�ij���
��3��ֱ��y��mx��m��0���뷴����������ͼ������������A��B����AB��10��ֱ��д��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ�˽����ѧ��ÿ����У�������ʱ�䣨��λ��h������������˸�У�IJ��ֳ���ѧ�������ݵ����������Ƴ����µ�ͳ��ͼ1��ͼ2������������Ϣ������������⣺
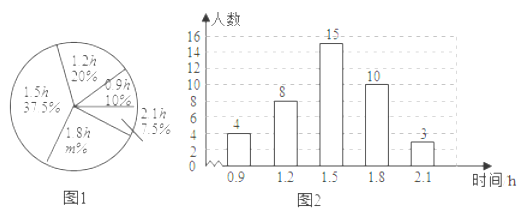
�����ν��ܵ���ij���ѧ������Ϊ�� ����ͼ1��m��ֵΪ�� ����
������ͳ�Ƶ�����ÿ����У�����ʱ�����ݵ���������λ����
������ͳ�Ƶ�����ÿ����У�����ʱ����������ݣ�����У����1200������ѧ�������Ƹ�Уÿ����У�����ʱ�����1h��ѧ��������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com