
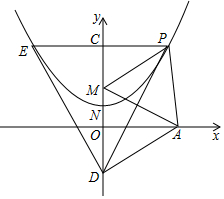
 ��ͼ����֪�����ߵĶԳ�����y�ᣬ�ҵ㣨2��2������1��$\frac{5}{4}$�����������ϣ���P���������ϲ��붥��N�غϵ�һ���㣬��P��PA��x����A��PC��y����C���ӳ�PC����������E����M��O���������߶���N�ĶԳƵ㣬D��C�����N�ĶԳƵ㣮
��ͼ����֪�����ߵĶԳ�����y�ᣬ�ҵ㣨2��2������1��$\frac{5}{4}$�����������ϣ���P���������ϲ��붥��N�غϵ�һ���㣬��P��PA��x����A��PC��y����C���ӳ�PC����������E����M��O���������߶���N�ĶԳƵ㣬D��C�����N�ĶԳƵ㣮���� ��1������֪������꣬���ô���ϵ��������������ߵĽ���ʽ��������䶥��N�����ꣻ
��2����P�������Ϊt����ɱ�ʾ��C��D��M��A�����꣬�Ӷ��ɱ�ʾ��PA��DM�ij�����PA=DM��֤�ý��ۣ�
��3����P�������Ϊt����Rt��PCM�У��ɱ�ʾ��PM�������PM=PA����֪�ı���PMDAΪ���Σ������ε����ʺ������ߵĶԳ��Կɵá�PDE=��APM����֤�ý��ۣ���Rt��AOM�У���t��ʾ��AM�ij����ٱ�ʾ��PE�ij��������Ʊ�Ϊ$\sqrt{3}$�ɵõ�����t�ķ��̣������t��ֵ�������P�����꣮
��� ��1���⣺�������ߵĶԳ�����y�ᣬ
����������߽���ʽΪy=ax2+c��
�ߵ㣨2��2������1��$\frac{5}{4}$�����������ϣ�
��$\left\{\begin{array}{l}{4a+c=2}\\{a+c=\frac{5}{4}}\end{array}\right.$�����$\left\{\begin{array}{l}{a=\frac{1}{4}}\\{c=1}\end{array}\right.$��
�������߽���ʽΪy=$\frac{1}{4}$x2+1��
��N��������0��1����
��2��֤������P��t��$\frac{1}{4}$t2+1������C��0��$\frac{1}{4}$t2+1����PA=$\frac{1}{4}$t2+1��
��M��O���������߶���N�ĶԳƵ㣬D��C�����N�ĶԳƵ㣬��N��0��1����
��M��0��2����
��OC=$\frac{1}{4}$t2+1��ON=1��
��DM=CN=$\frac{1}{4}$t2+1-1=$\frac{1}{4}$t2��
��OD=$\frac{1}{4}$t2-1��
��D��0��-$\frac{1}{4}$t2+1����
��DM=2-��-$\frac{1}{4}$t2+1��=$\frac{1}{4}$t2+1=PA����PM��DM��
���ı���PMDAΪƽ���ı��Σ�
��3���⣺ͬ��2����P��t��$\frac{1}{4}$t2+1������C��0��$\frac{1}{4}$t2+1����PA=$\frac{1}{4}$t2+1��PC=|t|��
��M��0��2����
��CM=$\frac{1}{4}$t2+1-2=$\frac{1}{4}$t2-1��
��Rt��PMC�У��ɹ��ɶ����ɵ�PM=$\sqrt{P{C}^{2}+C{M}^{2}}$=$\sqrt{{t}^{2}+��\frac{1}{4}{t}^{2}-1��^{2}}$=$\sqrt{��\frac{1}{4}{t}^{2}+1��^{2}}$=$\frac{1}{4}$t2+1=PA�����ı���PMDAΪƽ���ı��Σ�
���ı���PMDAΪ���Σ�
���APM=��ADM=2��PDM��
��PE��y�ᣬ�������߶Գ���Ϊy�ᣬ
��DP=DE���ҡ�PDE=2��PDM��
���PDE=��APM����$\frac{PD}{PA}$=$\frac{DE}{PM}$��
���DPE�ס�PAM��
��OA=|t|��OM=2��
��AM=$\sqrt{{t}^{2}+4}$����PE=2PC=2|t|��
�����Ʊ�Ϊ$\sqrt{3}$ʱ����$\frac{PE}{AM}$=$\sqrt{3}$����$\frac{2|t|}{\sqrt{{t}^{2}+4}}$=$\sqrt{3}$�����t=2$\sqrt{3}$��t=-2$\sqrt{3}$��
��P��������2$\sqrt{3}$��4����-2$\sqrt{3}$��4����
���� ����Ϊ���κ������ۺ�Ӧ�ã��漰����ϵ������ƽ���ı��ε��ж������ʡ����ɶ��������ε��ж������ʡ����������ε��ж������ʼ�����˼���֪ʶ���ڣ�1����ע�������߽���ʽ���跨���ڣ�2������t��ʾ��DM�ij��ǽ���Ĺؼ����ڣ�3����֤���ı���PMDAΪ�����ǽ���Ĺؼ������⿼��֪ʶ��϶࣬�ۺ��Խ�ǿ���������ϴ��ѶȽϴ�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
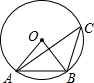 ��ͼ����A��B��C���ڡ�O�ϣ��ҵ�C����AB���Ե��Ż��ϣ������AOB=64�㣬��ô��ACB�Ķ����ǣ�������
��ͼ����A��B��C���ڡ�O�ϣ��ҵ�C����AB���Ե��Ż��ϣ������AOB=64�㣬��ô��ACB�Ķ����ǣ�������| A�� | 26�� | B�� | 30�� | C�� | 32�� | D�� | 64�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=2��x-3��2-5 | B�� | y=2��x+3��2+5 | C�� | y=2��x-3��2+5 | D�� | y=2��x+3��2-5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��3��-2�� | B�� | ��3��2�� | C�� | ��-3��-2�� | D�� | ��2��-3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com