
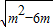 x-m+2=0有两个相等的实数根,则m= .
x-m+2=0有两个相等的实数根,则m= .  x-m+2=0有两个相等的实数根,得到m2-6m≥0,△=0,即△=(-
x-m+2=0有两个相等的实数根,得到m2-6m≥0,△=0,即△=(-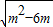 )2-4×1×(-m+2)=m2-2m-8=0,解方程m2-2m-8=0得x1=4,x2=-2;而x=4不满足m2-6m≥0,故舍去.最后得到m=-2.
)2-4×1×(-m+2)=m2-2m-8=0,解方程m2-2m-8=0得x1=4,x2=-2;而x=4不满足m2-6m≥0,故舍去.最后得到m=-2. x-m+2=0有两个相等的实数根,
x-m+2=0有两个相等的实数根, )2-4×1×(-m+2)=m2-2m-8=0,(m+2)(m-4)=0,所以m=-2或4;
)2-4×1×(-m+2)=m2-2m-8=0,(m+2)(m-4)=0,所以m=-2或4;

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com