(2009•娄底)已知关于x的二次函数y=x2-(2m-1)x+m2+3m+4.
(1)探究m满足什么条件时,二次函数y的图象与x轴的交点的个数;
(2)设二次函数y的图象与x轴的交点为A(x1,0),B(x2,0),且x12+x22=5,与y轴的交点为C,它的顶点为M,求直线CM的解析式.
【答案】
分析:(1)由△=b
2-4ac可写出用m表示的△关系式,分别讨论m在取不同的值时二次函数y的图象与x轴的交点的个数;
(2)由根与系数的关系可把x
12+x
22转换为m的表达式,由此可得方程2m
2-10m-7=5,求出m的值可得二次函数解析式;则根据函数表达式可求出顶点M及与y轴交点C的坐标,使用代入法可求得直线CM的解析式.
解答:解:(1)令y=0,得:x
2-(2m-1)x+m
2+3m+4=0,
∴△=(2m-1)
2-4(m
2+3m+4)=-16m-15,
当△>0时,方程有两个不相等的实数根,即-16m-15>0,
∴m<-

,
此时y的图象与x轴有两个交点;
当△=0时,方程有两个相等的实数根,即-16m-15=0,
∴m=-
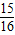
,
此时,y的图象与x轴只有一个交点;
当△<0时,方程没有实数根,即-16m-15<0,
∴m>-

,
此时y的图象与x轴没有交点.
∴当m<-

时,y的图象与x轴有两个交点;
当m=-

时,y的图象与x轴只有一个交点;
当m>-

时,y的图象与x轴没有交点.
(2)由根与系数的关系得x
1+x
2=2m-1,x
1x
2=m
2+3m+4,
∴x
12+x
22=(x
1+x
2)
2-2x
1x
2=(2m-1)
2-2(m
2+3m+4)=2m
2-10m-7,
∵x
12+x
22=5,
∴2m
2-10m-7=5,
∴m
2-5m-6=0,
解得:m
1=6,m
2=-1,
∵m<-

,
∴m=-1,
∴y=x
2+3x+2,
令x=0,得y=2,
∴二次函数y的图象与y轴的交点C坐标为(0,2),
又y=x
2+3x+2=(x+

)
2-

,
∴顶点M的坐标为(-

,-

),
设过C(0,2)与M(-

,-

)的直线解析式为y=kx+b,
解得k=

,b=2,
∴所求的解析式为y=

x+2.
点评:本题考查了一元二次方程中△的应用,考查了学生分类讨论问题的能力;需注意灵活运用一元二次方程中根与系数的关系的求函数解析式;求函数解析式一般要用待定系数法.

 ,
,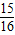 ,
, ,
, 时,y的图象与x轴有两个交点;
时,y的图象与x轴有两个交点; 时,y的图象与x轴只有一个交点;
时,y的图象与x轴只有一个交点; 时,y的图象与x轴没有交点.
时,y的图象与x轴没有交点. ,
, )2-
)2- ,
, ,-
,- ),
), ,-
,- )的直线解析式为y=kx+b,
)的直线解析式为y=kx+b, ,b=2,
,b=2, x+2.
x+2.

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案