
����Ŀ����ͼ��ֱ��l�Ľ���ʽΪy=![]() x+b������������ֱ���A��B���㣬����B����Ϊ��0��4����
x+b������������ֱ���A��B���㣬����B����Ϊ��0��4����
��1�����A������ꣻ
��2������ P��y���ϣ��ҵ�ֱ��l�ľ���Ϊ3�������P�����ꣻ
��3���ڵ�һ���Ľ�ƽ�������Ƿ���ڵ�Qʹ�á�QBA=90���������ڣ����Q�����ꣻ�������ڣ���˵�����ɣ�
��4������C��y���ϵĵ㣨0��10����������ÿ��1cm���ٶ���y�Ḻ���᷽���˶��������C�˶������п�����ʱ��tֵ��ʹ����ABCΪ��Գ�ͼ�Σ�

���𰸡���1��A��3��0������2��P��0��9����0����1������3�����ڣ���16��16������4��1�롢![]() �롢11�롢14��
�롢11�롢14��
�������������������1�����õ�B����ֱ�ߣ����ֱ�߽���ʽ��Ȼ����ֱ����x�ύ�����ꣻ
��2����֪�㵽ֱ�߾��룬�������㵽ֱ�ߵĴ��ߣ�����ֱ�������Σ��������������ƾͳ���Ӧ�߶γ��ȣ��̶����������ꣻ
��3����Q�ڵ�һ����ƽ�����ϣ���Q��x��x������֪������ָ���ǣ����ù��ɶ����з��̣����������Q�����ꣻ
��4����Ŀ����ABCΪ��Գ�ͼ�Σ�ʵ������C��ʹ��ABCΪ���������Σ����ݵ������������ʷ������ۼ������������꣬���õ����������˶�ʱ�䣮
����������⣺��1������B��0��4������ֱ��l�Ľ���ʽ�ã�b=4����ֱ��l�Ľ���ʽΪ��y=![]() x+4����y=0�ã�x=3����A��3��0����
x+4����y=0�ã�x=3����A��3��0����
��2����ͼ������P��ֱ��AB�Ĵ��ߣ�����ΪD����OB=4��OA=3����AB=5���ߡ�B�ǹ����ǣ���BDP=��BOD�����BOA�ס�BDP���� ![]() ����
����![]() ����BP=5��4+5=9��4��5=��1����P��0��9����0����1����
����BP=5��4+5=9��4��5=��1����P��0��9����0����1����
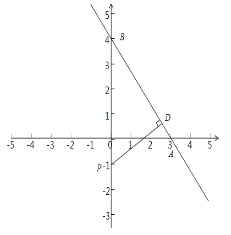
��3�����ڣ���Q�ڵ�һ���Ľ�ƽ�����ϣ���Q��x��x�������ݹ��ɶ�����
QB2+BD2=QD2��x2+��x��4��2+52=x2+��x��3��2�����x=16����Q��16��16����
��4����ʹ��ABCΪ��Գ�ͼ�Σ���ã���ABCΪ���������Σ���AB=BCʱ��C��0��9����0����1������ʱC���˶�1���11�룬��AB=ACʱ��C��0����4������ʱC���˶�14�룬��AC=BCʱ��C��0�� ![]() ������ʱC���˶�
������ʱC���˶�![]() �룮
�룮
������������C���˶�1�롢![]() �롢11�롢14��ʱ����ʹ��ABCΪ��Գ�ͼ�Σ�
�롢11�롢14��ʱ����ʹ��ABCΪ��Գ�ͼ�Σ�


 ���ѵ����Ԫ��ĩ���100��ϵ�д�
���ѵ����Ԫ��ĩ���100��ϵ�д� ��˼άС�ھ�100����ҵ��ϵ�д�
��˼άС�ھ�100����ҵ��ϵ�д� ��ʦָ��һ��ͨϵ�д�
��ʦָ��һ��ͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������Ĵ�����װ�н���ɫ��ͬ��10��С�����к���4��������6����
(1)�ȴӴ�����ȡ��m(m��1)�������ٴӴ������������1������������������Ϊ�¼�A����������б���
![]()
(2)�ȴӴ�����ȡ��m�������ٷ���m��һ���ĺ���ҡ�ȣ��������1������ĸ��ʵ���![]() ����m��ֵ��
����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������л�ʫ�ʣ�Ѱ�Ļ�����Ʒ����֮������ijУ�ٰ����조�й�ʫ�ʴ�ᡱ����ѡ�κ���50��ѧ���μӾ�������50��ѧ��ͬʱĬд50��ʫ�ʣ���ÿ��ȷĬд��һ��ʫ�ʵ�2�֣����ݲ��Գɼ����Ƴ�����Ƶ���ֲ����Ͳ���Ƶ���ֲ�ֱ��ͼ��ͼ����
����ͼ��������и��⣺
��1���ٱ���a��ֵΪ �� ��λ���ڵ��飻
��Ƶ���ֲ�ֱ��ͼ����������
��2�������Գɼ�������80��Ϊ���㣬�β��Ե��������Ƕ��٣�
��3����5��10��ͬѧ�У���4����ͬѧ���ֽ���10��ͬѧƽ���ֳ�������жԿ���ϰ����4����ͬѧÿ������ˣ���С����Сǿ������ͬѧ�ܷ���ͬһ��ĸ��ʣ�
��� | �ɼ�x�� | Ƶ���������� |
��1�� | 50��x��60 | 6 |
��2�� | 60��x��70 | 8 |
��3�� | 70��x��80 | 14 |
��4�� | 80��x��90 | a |
��5�� | 90��x��100 | 10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijũ��300��ְ������51��������,�ƻ���ֲˮ��,�����߲�,��֪��ֲũ����ÿ����������Ͷ���������Ͷ����豸�ʽ����±���
ũ����Ʒ�� | ÿ�������Ͷ��� | ÿ������Ͷ���ʽ� |
ˮ�� | 4�� | 1��Ԫ |
�� | 8�� | 1��Ԫ |
�߲� | 5�� | 2��Ԫ |
��֪��ũ���ƻ����豸��Ͷ��67��Ԫ,Ӧ��������������ũ�������ֲ���,����ʹ���е�ְ�����й���,����Ͷ����ʽ����ù��ã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�Dz��ȱ������Σ� ![]() ����
����![]() ��
�� ![]() Ϊ����������λ�ò�ͬ�������Σ�ʹ������DEF����ABCȫ�ȣ������������������Ի����� ��
Ϊ����������λ�ò�ͬ�������Σ�ʹ������DEF����ABCȫ�ȣ������������������Ի����� ��

A. ![]() �� B.
�� B. ![]() �� C.
�� C. ![]() �� D.
�� D. ![]() ��
��
���𰸡�B
�������������������ͼ����������������������4��.

��ѡB.
�����͡���ѡ��
��������
9
����Ŀ�����������õ��Ļ�����ͼ�ǣ�
��1��___________________________����2��_______________________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���ACB=90����AC=BC���ӳ�AB����D��ʹDB=AB������CD����CDΪֱ�DZ�������ֱ��������CDE��������DCE=90��������BE.
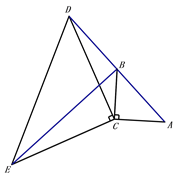
��1����֤����ACD�ա�BCE��
��2) ��AC=3cm����BE�ij���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������õ��Ļ�����ͼ�ǣ�
��1��___________________________����2��_______________________________��
���𰸡� ��һ���ǵ�����֪�� ��һ���߶ε�����֪�߶�
��������������������������õ��Ļ�����ͼ�ǣ�(1). ��һ���ǵ�����֪��(2). ��һ���߶ε�����֪�߶�
�ʴ�Ϊ��(1). ��һ���ǵ�����֪��(2). ��һ���߶ε�����֪�߶�.
�����͡������
��������
10
����Ŀ���߹��������ε����ͣ�
�� �� �� ͼ | ���� | ���� |
��֪������н��������� | __________ | |
��֪����һ���������� | __________���� | |
��֪������������ | __________ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ʵ����������з��̣�
��1����3x+1��2��9=0
��2��x2+4x��1=0
��3��3x2��2=4x
��4����y+2��2=1+2y��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com