
【题目】如图,四边形ABCD中,∠ABC+∠D=180°,AC平分∠BAD,CE⊥AB,CF⊥AD.试说明:
(1)△CBE≌△CDF;
(2)AB+DF=AF.

【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)根据角平分线的性质可得到CE=CF,根据余角的性质可得到∠EBC=∠D,已知CE⊥AB,CF⊥AD,从而利用AAS即可判定△CBE≌△CDF.
(2)已知EC=CF,AC=AC,则根据HL判定△ACE≌△ACF得AE=AF,最后证得AB+DF=AF即可.
试题解析:证明:(1)∵AC平分∠BAD,CE⊥AB,CF⊥AD
∴CE=CF
∵∠ABC+∠D=180°,∠ABC+∠EBC=180°
∴∠EBC=∠D
在△CBE与△CDF中,
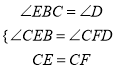 ,
,
∴△CBE≌△CDF;
(2)在Rt△ACE与Rt△ACF中,
![]()
∴△ACE≌△ACF
∴AE=AF
∴AB+DF=AB+BE=AE=AF.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】下列说法:①如果两个数的和为1,则这两个数互为倒数;②如果两个数积为0,则至少有一个数为0;③绝对值是本身的有理数只有0;④倒数是本身的数是-1,0,1。其中错误的个数是( )
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等腰△ABC的周长为8,腰长为x,底边长为y.
(1)写出y关于x的函数关系式,并求自变量x的取值范围;
(2)在平面直角坐标系中,画出y与x之间的函数图像;
(3)若△ABC的三边长均为整数,求三边的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=4cm, BC=12cm.点P从点C处出发以1cm/s向A匀速运动,同时点Q从B点出发以2cm/s向C点匀速移动,若一个点到达目的停止运动时,另一点也随之停止运动.运动时间为t秒;

(1)用含有t的代数式表示BQ、CP的长;
(2)写出t的取值范围;
(3)用含有t的代数式 表示Rt△PCQ和四边形APQB的面积;
(4)当P、Q处在什么位置时,四边形PQBA的面积最小,并求这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每个小正方形边长都是![]() ,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
(![]() )画一个三角形,使它的三边长都是有理数.
)画一个三角形,使它的三边长都是有理数.
(![]() )画一个直角三角形,使它们的三边长都是无理数.
)画一个直角三角形,使它们的三边长都是无理数.
(![]() )画出与
)画出与![]() 成轴对称且与
成轴对称且与![]() 有公共点的格点三角形(画出一个即可).
有公共点的格点三角形(画出一个即可).



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com