
分析 (1)根据根据勾股定理和三角函数的定义即可得到结论;
(2)根据三角形的内角和得到∠A,∠B,然后根据直角三角形的性质即可得到结论.
解答 解:(1)∵a=$2\sqrt{6}$,c=7,
∴b=$\sqrt{{c}^{2}-{a}^{2}}$=5,
∵sinB=$\frac{b}{c}$=$\frac{5}{7}$≈0.7143,
∴∠B=45.81°,
∴∠A=54.19°;
(2)∵∠A-∠B=30°,∠A+∠B=90°,
∴∠A=60°,∠B=30°,
∴c=2b,
∵b+c=24,
∴b=8,c=16,a=8$\sqrt{3}$.
点评 本题考查了解直角三角形,主要利用了锐角三角函数和勾股定理.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
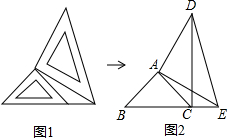 两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.
两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
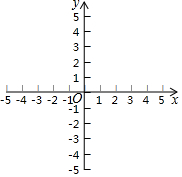 已知二次函数y=-x2+2x+3,
已知二次函数y=-x2+2x+3,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
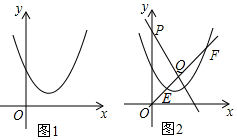 抛物线C1:y=ax2+bx+c(a>0)过y轴上一点(0,4).
抛物线C1:y=ax2+bx+c(a>0)过y轴上一点(0,4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
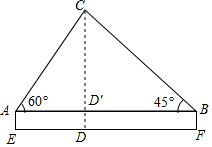 从相距100m的A,B两点观侧建筑物CD,用测角仪测得建筑物顶点CA体的高度的仰角分别为60°和45°,求E,F两点到建筑物底端D的距离分别为多少米.
从相距100m的A,B两点观侧建筑物CD,用测角仪测得建筑物顶点CA体的高度的仰角分别为60°和45°,求E,F两点到建筑物底端D的距离分别为多少米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com