Question

某服装公司试销一种成本为每件50元的T恤衫，规定试销时的销售单价不低于成本价，又不高于每件70元，试销中销售量y(件)与销售单价x(元)的关系可以近似地看作一次函数(如图)．

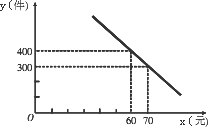
(1)求y与x之间的函数表达式；

(2)设公司获得的总利润(总利润＝总销售额－总成本)为P元，求P与x之间的函数表达式，并写出自变量x的取值范围；根据题意判断：当x取何值时，P的值最大？最大值是多少？

Answer 1

答案：
解析：

分析：(1)根据函数图象获得信息，求出一次函数表达式；(2)与母题一样，首先确定总利润P的函数表达式，然后再求最大值．不同之处是本题顶点横坐标不在自变量的取值范围内时，需根据二次函数的增减性求最大值． 　　解：(1)设y与x之间的函数表达式为y＝kx＋b． 　　因为y＝kx＋b经过点(60，400)、(70，300)， 　　所以解得 　　所以y与x之间的函数表达式为y＝－10x＋1000． 　　(2)P＝(－10x＋1000)(x－50) 　　＝－10x2＋1500x－50000， 　　自变量x的取值范围是50≤x≤70． 　　因为－＝－＝75，a＜0， 　　所以函数P＝－10x2＋1500x－50000的图象开口向下，对称轴为x＝75． 　　因为50≤x≤70，此时y随x的增大而增大， 　　所以当x＝70时，P最大，最大利润为6000元． 　　点评：在实际问题中，最值不一定是二次函数的顶点纵坐标，需要根据自变量的取值范围确定．