
【题目】某学校组建了书法、音乐、美术、舞蹈、演讲五个社团,全校每一名学生都参加且只参加了其中一个社团的活动.校团委从全校学生中随机选取部分学生进行了参加活动情况的调查,并将调查结果制成了如图不完整的统计图.请根据统计图完成下列问题:
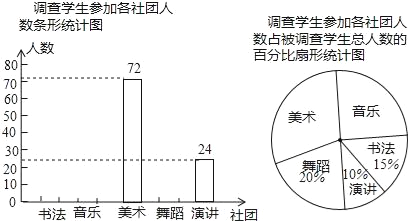
(1)参加本次调查有 名学生?
(2)根据调查数据分析,被调查的学生中有 名学生参加了音乐社团?
(3)请你补全条形统计图.
【答案】(1)240;(2)60;(3)见解析.
【解析】
(1) 根据 “演讲” 社团的24个人占被调查人数的10%可得总人数;
(2) 将总人数分别乘以 “书法”、 “舞蹈” 的百分比求出其人数,将总人数减去其余四个社团的人数可得“音乐”社团的人数;
(3) 根据以上数据即可补全条形图.
解:(1)参加本次调查的学生人数为24÷10%=240人,
故答案为:240;
(2)∵参加“书法”社团的人数为:240×15%=36(人),
参加“舞蹈”社团的人数为:240×20%=48(人),
∴参加“音乐”社团的人数为:240﹣36﹣72﹣48﹣24=60(人),
故答案为:60;
(3)补全条形图如图:


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
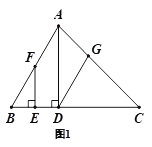
【题目】已知,在三角形ABC中,AD⊥BC于D,F是AB上一点,FE⊥BC于E,∠ADG=∠BFE
(1)如图1,求证:DG∥AB
(2)如图2,若∠BAC=90°,请直接写出图中与∠CAD互余的角,不需要证明.
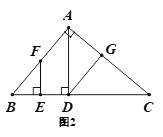
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为原点,一次函数与反比例函数的图象相交于A(2,1)、B(﹣1,﹣2)两点,与x轴交于点C. 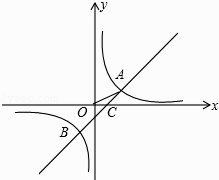
(1)分别求反比例函数和一次函数的解析式(关系式);
(2)连接OA,求△AOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣2x+10与x轴,y轴相交于A,B两点,点C的坐标是(8,4),连接AC,BC.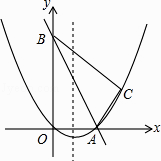
(1)求过O,A,C三点的抛物线的解析式,并判断△ABC的形状;
(2)动点P从点O出发,沿OB以每秒2个单位长度的速度向点B运动;同时,动点Q从点B出发,沿BC以每秒1个单位长度的速度向点C运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为t秒,当t为何值时,PA=QA?
(3)在抛物线的对称轴上,是否存在点M,使以A,B,M为顶点的三角形是等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=120°,BC=6cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为( ) 
A.4cm
B.3cm
C.2cm
D.1cm
查看答案和解析>>
科目:初中数学 来源: 题型:
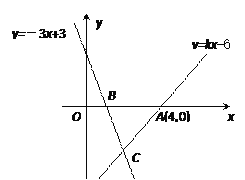
【题目】如图,直线y=kx-6经过点A(4,0),直线y=-3x+3与x轴交于点B,且两直线交于点C.
(1)求k的值.
(2)求△ABC的面积.
(3)在直线y=kx-6上是否存在异于点C的另一点P,使得△ABP与△ABC的面积相等,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)化简: ![]() (2)解方程:
(2)解方程:![]() .
.
【答案】(1) ![]() 或
或![]() ;(2)x=-2.
;(2)x=-2.
【解析】(1)先把括号内通分,再把除法转化为乘法,并把分子、分母分解因式约分化简;
(2)两边都乘以最简公分母2(x+3),把分式方程化为整式方程求解,求出x的值不要忘记检验.
(1)原式=![]() =
=![]() =
=![]() 或
或![]() ;
;
(2)解:去分母得:![]() ,
,
解得:x=﹣2,
经检验x=﹣2是分式方程的解,
∴原方程的解为x=﹣2
点睛:本题考查了分式的混合运算和解分式方程,熟练掌握分式的运算法则和解分式方程的方法是解答本题的关键.
【题型】解答题
【结束】
20
【题目】小张同学学完统计知识后,随机调查了她所在辖区若干名居民的年龄,将调查数据绘制成如下扇形统计图和条形统计图:

请根据以上不完整的统计图提供的信息,解答下列问题:
(1)小张同学共调查了 名居民的年龄,扇形统计图中a= ;
(2)补全条形统计图,并注明人数;
(3)若在该辖区中随机抽取一人,那么这个人年龄是60岁及以上的概率为 ;
(4)若该辖区年龄在0~14岁的居民约有2400人,请估计该辖区居民有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
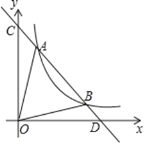
【题目】如图,一次函数![]() 分别交y轴、x轴于C、D两点,与反比例函数y=
分别交y轴、x轴于C、D两点,与反比例函数y=![]() (x>0)的图象交于A(m,8),B(4,n)两点.
(x>0)的图象交于A(m,8),B(4,n)两点.
(1)求反比例函数的解析式;
(2)根据图象直接写出![]() <
<![]() 的x的取值范围;
的x的取值范围;
(3)求![]() 的面积.
的面积.
【答案】(1)y=![]() ;(2)
;(2) ![]() 或
或![]() ;(3)15.
;(3)15.
【解析】(1)把B(4,n)两点分别代入![]() 可求出n的值,确定B点坐标为B(4,2),后利用待定系数法求反比例函数的解析式;
可求出n的值,确定B点坐标为B(4,2),后利用待定系数法求反比例函数的解析式;
(2)观察函数图象得到当![]() 或
或![]() ,反比例函数的图象在一次函数图象上方.
,反比例函数的图象在一次函数图象上方.
(3)求得直线![]() 与坐标轴轴的交点坐标,根据三角形面积公式即可求得.
与坐标轴轴的交点坐标,根据三角形面积公式即可求得.
(1)将![]() 代入
代入![]() 得
得![]() ,
,
得反比例函数的关系式是![]() .
.
(2)![]() 或
或![]() ,
,
(3)![]() 点的坐标是(0,10),
点的坐标是(0,10),![]() 点的坐标是(5,0),
点的坐标是(5,0),
分别过点A、B两点作![]() 轴、
轴、![]() 轴的垂线段,
轴的垂线段,
![]() .
.
点睛:本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数的解析式.也考查了待定系数法求函数的解析式以及观察图象的能力.
【题型】解答题
【结束】
25
【题目】探索发现:![]() ;
;![]() ;
;![]() …根据你发现的规律,回答下列问题
…根据你发现的规律,回答下列问题
(1)![]() ,
,![]() ;
;
(2)利用你发现的规律计算:![]() ;
;
(3)灵活利用规律解方程:
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店用 6000 元购进一批衬衫,以 60 元/件的价格出售,很快售完,然后又用 13500元购进同款衬衫,购进数量是第一次的 2 倍,购进的单价比上一次每件多 5 元,服装店 仍按原售价 60 元/件出售,并且全部售完.
(1)该服装店第一次购进衬衫多少件?
(2)将该服装店两次购进衬衫看作一笔生意,那么这笔生意是盈利还是亏损?求出盈利(或 亏损)多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com