

 和8+2
和8+2

 ,
, =
= ,
, =
= ,
, ,
, ,BE=4﹣
,BE=4﹣ ,
, ×(4﹣
×(4﹣ )×4=8﹣2
)×4=8﹣2 ,
, ×(4+
×(4+ )×4=8+2
)×4=8+2 ,
, 和8+2
和8+2 .
.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 (x>0)的图象上.
(x>0)的图象上.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 旋钮角度(度) | 20 | 50 | 70 | 80 | 90 |
| 所用燃气量(升) | 73 | 67 | 83 | 97 | 115 |

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 (m≠0)的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.
(m≠0)的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 的图象没有公共点,则( )
的图象没有公共点,则( )| A.k1+k2<0 | B.k1+k2>0 | C.k1k2<0 | D.k1k2>0 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,
,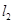 相交于点
相交于点 ,
, 与
与 轴的交点坐标为
轴的交点坐标为 ,
,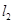 与
与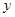 轴的交点坐标为
轴的交点坐标为 ,结合图象解答下列问题:(每小题4分,共8分)
,结合图象解答下列问题:(每小题4分,共8分)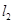 表示的一次函数的表达式;
表示的一次函数的表达式; 为何值时,
为何值时, ,
,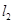 表示的两个一次函数值都大于
表示的两个一次函数值都大于 .
.
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
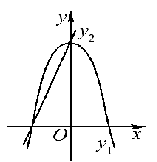
 或
或 .
.| A.①② | B.①④ | C.②③ | D.③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com