Question

方程3x²+7xy-2x-5y-35=0的不同正整数解（x₁，y₁），（x₂，y₂），…，（x_n，y_n），中x₁+x₂+x₃+…+x_n=    ．

Answer 1

【答案】分析：把所给方程整理为用x表示成y的形式，整理为含有7x-5的形式，化简后判断正整数解即可．
解答：解：由3x²+7xy-2x-5y-35=0可知，y=，
∴，
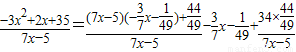
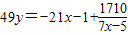
∴（7x-5）|1710=2×3²×5×19，
∴x≥1，y≥1，知7x-5＞0，
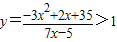
∴3x²+5x-40＜0，
∴x＜3，
∴x₁=1，y₁=17；或x₂=2，y₂=3，
∴只有两组解，故x₁+x₂=3．
故答案为3．
点评：考查二次方程的整数解；用一个字母表示出另一个字母是解决本题的关键；把相关式子化简为一个整式与一个分式的和的形式是解决本题的难点．