
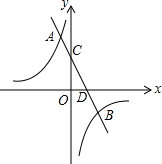
 如图,在平面直角坐标系xOy中,一次函数y=k1x+b与反比例函数y=$\frac{{k}_{2}}{x}$的图象交于点A(-1,6)和点B(3,m),与y轴交于点C,与x轴交于点D.
如图,在平面直角坐标系xOy中,一次函数y=k1x+b与反比例函数y=$\frac{{k}_{2}}{x}$的图象交于点A(-1,6)和点B(3,m),与y轴交于点C,与x轴交于点D.分析 (1)将A坐标代入反比例函数解析式中求出k2的值,即可确定出反比例函数解析式;将B坐标代入反比例解析式中求出m的值,确定出B坐标,将A与B坐标代入一次函数解析式中求出k1与b的值,即可确定出一次函数解析式;
(2)如图,当P在第二象限时,连接PC,PO,作PE⊥y轴于E,求得D的横坐标为2,根据已知条件得到PE=OD=2,求得P的横坐标为-2,把x=-2代入y=-$\frac{6}{x}$中得y=3,于是得到结论;同理可得当点P在第四象限时,求得P(2,-3).
解答  解:∵A(-1,6)在y=$\frac{{k}_{2}}{x}$上得k2=-6.
解:∵A(-1,6)在y=$\frac{{k}_{2}}{x}$上得k2=-6.
∴y=-$\frac{6}{x}$,
∵B(3,m)反比例函数y=-$\frac{6}{x}$的图象上,
∴m=-2,
因为y=k1x+b过A(-1,6)、B(3,-2)两点,
∴$\left\{\begin{array}{l}{6=-{k}_{1}+b}\\{-2=3{k}_{1}+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{1}=-2}\\{b=4}\end{array}\right.$,
∴一次函数的表达式是y=-2x+4;
(2)如图,当P在第二象限时,连接PC,PO,作PE⊥y轴于E,把y=0代入y=-2k+4中得x=2,
∴D的横坐标为2,
∵S△PCD=S△DOC,
∴$\frac{1}{2}$CO•PE=$\frac{1}{2}$CO•OD,
∴PE=OD=2,
∴P的横坐标为-2,
把x=-2代入y=-$\frac{6}{x}$中得y=3,
∴此时点P的坐标为(-2,3),
同理可得当点P在第四象限时,P(2,-3),
∴点P的坐标是(-2,3),(2,-3).
点评 此题考查了一次函数与反比例函数的交点问题,涉及的知识有:待定系数法求函数解析式,坐标与图形性质,熟练掌握待定系数法是解本题的关键.


科目:初中数学 来源: 题型:选择题
 如图,?ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO、BO的中点.若AC+BD=24cm,EF的长为3cm,则△OAB的周长是( )
如图,?ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO、BO的中点.若AC+BD=24cm,EF的长为3cm,则△OAB的周长是( )| A. | 16cm | B. | 18cm | C. | 20cm | D. | 22cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
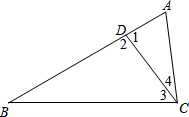 如图,△ABC中,D为AB上一点.已知△ADC与△DBC的面积比为1:3,且AD=3,AC=6,请求出BD的长度,并完整说明为何∠ACD=∠B的理由.
如图,△ABC中,D为AB上一点.已知△ADC与△DBC的面积比为1:3,且AD=3,AC=6,请求出BD的长度,并完整说明为何∠ACD=∠B的理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
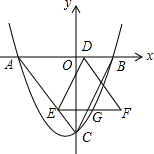 如图,抛物线y=ax2+bx-4经过A(-3,0)、B(2,0)两点,与y轴的交点为C,连接AC、BC,D为线段AB上的动点,DE∥BC交AC于E,A关于DE的对称点为F,连接DF、EF.
如图,抛物线y=ax2+bx-4经过A(-3,0)、B(2,0)两点,与y轴的交点为C,连接AC、BC,D为线段AB上的动点,DE∥BC交AC于E,A关于DE的对称点为F,连接DF、EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com