
科目:初中数学 来源: 题型:选择题
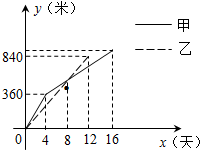 我市某县在实施“村村通”工程中,决定在A、B两村之间修筑一条公路,甲、乙两个工程队分别从A、B两村同时相向开始修筑.乙队修筑了840米后,因另有任务提前离开,余下的任务由甲队单独完成,直到道路修通.两队开工8天时,所修道路的长度都为560米,甲、乙两个工程队所修道路的长度y(米)与修筑时间x(天)之间的关系图象如图所示.下列说法:
我市某县在实施“村村通”工程中,决定在A、B两村之间修筑一条公路,甲、乙两个工程队分别从A、B两村同时相向开始修筑.乙队修筑了840米后,因另有任务提前离开,余下的任务由甲队单独完成,直到道路修通.两队开工8天时,所修道路的长度都为560米,甲、乙两个工程队所修道路的长度y(米)与修筑时间x(天)之间的关系图象如图所示.下列说法:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{22}{7}$ | B. | 1.6$\stackrel{•}{7}$ | C. | 0.222222… | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
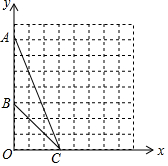 如图,在平面直角坐标系xOy中,点A的坐标为(0,7),点B的坐标为(0,3),点C的坐标为(3,0).
如图,在平面直角坐标系xOy中,点A的坐标为(0,7),点B的坐标为(0,3),点C的坐标为(3,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,BE,CF是△ABC的高,点P在BE上,点Q在CF的延长线上,BP=AC,CQ=AB,
如图,BE,CF是△ABC的高,点P在BE上,点Q在CF的延长线上,BP=AC,CQ=AB,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com