
【题目】已知:在![]() 中,
中,![]() 是
是![]() 边上的中线,点
边上的中线,点![]() 是
是![]() 的中点;过点
的中点;过点![]() 作
作![]() ,交
,交![]() 的延长线于
的延长线于![]() ,连接
,连接![]() .
.
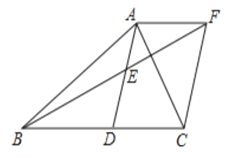
(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)当![]() 分别满足什么条件时,四边形
分别满足什么条件时,四边形![]() 是菱形;四边形
是菱形;四边形![]() 是矩形,并说明理由.
是矩形,并说明理由.
 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:初中数学 来源: 题型:
【题目】勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )

A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学初一年级有350名同学去春游,已知2辆A型车和1辆B型车可以载学生100人,1辆A型车和2辆B型车可以载学生110人.
(1)A、B型车每辆可分别载学生多少人?
(2)若计划租用A型车![]() 辆,租用B型车
辆,租用B型车![]() 辆,请你设计租车方案,能一次运送所有学生,且恰好每辆车都坐满.
辆,请你设计租车方案,能一次运送所有学生,且恰好每辆车都坐满.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点(﹣1,y1),(4,y2)在一次函数y=3x﹣2的图象上,则y1 , y2 , 0的大小关系是( )
A.0<y1<y2
B.y1<0<y2
C.y1<y2<0
D.y2<0<y1
查看答案和解析>>
科目:初中数学 来源: 题型:
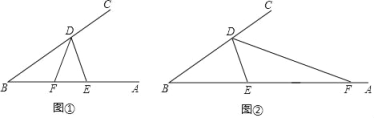
【题目】已知点D、E分别是∠B的两边BC、BA上的点,∠DEB=2∠B,F为BA上一点.
(1)如图①,若DF平分∠BDE,求证:BD=DE+EF;
(2)如图②,若DF为△DBE的外角平分线,BD、DE、EF三者有怎样的数量关系?请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
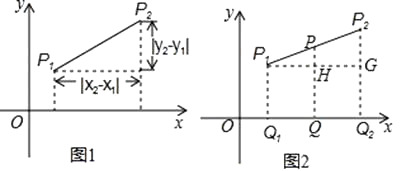
【题目】小明在求同一坐标轴上两点间的距离时发现,对于平面直角坐标系内任意两点P1(x1 , y1),P2(x2 , y2),可通过构造直角三角形利用图1得到结论:P1P2= ![]() 他还利用图2证明了线段P1P2的中点P(x,y)P的坐标公式:x=
他还利用图2证明了线段P1P2的中点P(x,y)P的坐标公式:x= ![]() ,y=
,y= ![]() .
.
(1)请你帮小明写出中点坐标公式的证明过程;
(2)①已知点M(2,﹣1),N(﹣3,5),则线段MN长度为;
②直接写出以点A(2,2),B(﹣2,0),C(3,﹣1),D为顶点的平行四边形顶点D的坐标:;
(3)如图3,点P(2,n)在函数y= ![]() x(x≥0)的图象OL与x轴正半轴夹角的平分线上,请在OL、x轴上分别找出点E、F,使△PEF的周长最小,简要叙述作图方法,并求出周长的最小值.
x(x≥0)的图象OL与x轴正半轴夹角的平分线上,请在OL、x轴上分别找出点E、F,使△PEF的周长最小,简要叙述作图方法,并求出周长的最小值.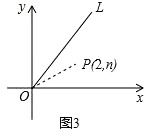
查看答案和解析>>
科目:初中数学 来源: 题型:
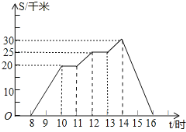
【题目】周末,小李8时骑自行车从家里出发,到野外郊游,16时回到家里.他离家的距离s(千米)与时间t(时)之间的关系可以用图中的折线表示.现有如下信息:
①小李到达离家最远的地方是14时;
②小李第一次休息时间是10时;
③11时到12时,小李骑了5千米;
④返回时,小李的平均速度是10千米/时.
其中,正确的有( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
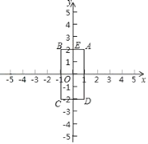
【题目】如图,已知四边形ABCD的顶点为A(1,2),B(﹣1,2),C,(﹣1,﹣2),D(1,﹣2),点M和点N同时从E点出发,沿四边形的边做环绕匀速运动,M点以1单位/s的速度做逆时针运动,N点以2单位/s的速度做顺时针运动,则点M和点N第2019次相遇时的坐标为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com