
����Ŀ����8�֣�ij�ֲ��ž����������е�349����ֻ��ܺ�295�����ֻ��ܴ���A��B����������50�����ڷ���ӭ��������࣮��֪����һ��A����������ֻ���8�裬���ֻ���4�裻����һ��B����������ֻ���5�裬���ֻ���9�裮
��l��ijУ2015����꼶ij�����С��н�����������ʹ��䷽������ƣ��ʷ�������Ĵ��䷽���м��֣����������Ƴ�����
��2��������һ��A�����͵ijɱ���200Ԫ������һ��B�����͵ijɱ���360Ԫ����˵����1�������ַ����ɱ���ͣ���ͳɱ��Ƕ���Ԫ��
���𰸡��⣺��1�������A������![]() ���������B������
���������B������![]() ������
������
![]()
��ã�![]()
��![]() ��������
��������
��![]() ����ȡ29,30,31,32,33.
����ȡ29,30,31,32,33.
���������ַ�����
����һ��A��29��B��21��
��������A��30��B��20��
��������A��31��B��19��
�����ģ�A��32��B��18��
�����壺A��33��B��17��
��2�������Ϊy����![]()
��![]() ����y��x�����������
����y��x�����������
����![]() ʱ����������ijɱ���ͣ���ͳɱ�=
ʱ����������ijɱ���ͣ���ͳɱ�=![]() ��
��
�����������⣨1��������Ŀ�е��������ȹ�ϵ��A����������ֻ��ܵ�����+B����������ֻ��ܵ�������349��A�����������ֻ��ܵ�����+B�����������ֻ��ܵ�������295���������г�һԪһ�β���ʽ�飬ֱ�ӽⲻ��ʽ�飬Ȼ��ȡ�����⼴�ɣ���2�������ַ�������������ɵã�B�����͵���۳ɱ�����A�����ͳɱ�������B������Խ�٣��ɱ�Խ�ͣ�����ѡ��B�������ٵķ�������������ַ����ijɱ����ɣ����ݣ�1���еó��ķ������ֱ�����ÿ�ַ����ijɱ���ѡ��ɱ���͵ķ������ɣ�
��������� �⣺��1�������A������x������B������Ϊ��50��x������
�������![]() ��
��
���������ʽ��ã�31��x��33��
��x��������
��x��ȡ31��32��33��
����������ִ��䷽�� ��A��������31����B��������19����
��A��������32����B��������18����
��A��������33����B��������17����
��2������һ������B�����͵���۳ɱ�����A�����ͳɱ�������B������Խ�٣��ɱ�Խ�ͣ�
��Ӧѡ�������ɱ���ͣ���ͳɱ�Ϊ33��200+17��360=12720��Ԫ����
����������������ɱ�31��200+19��360=13040��Ԫ����
��������ɱ�32��200+18��360=12880��Ԫ����
��������ɱ�33��200+17��360=12720��Ԫ����
��Ӧѡ�������ɱ���ͣ���ͳɱ�Ϊ12720Ԫ��


 ��ĩ�����ϵ�д�
��ĩ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
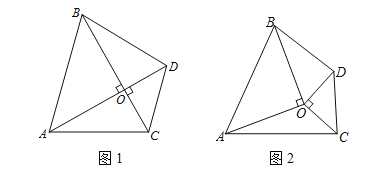
����Ŀ������OAB����OA��OB��OA��OB������OCD����OC��OD��OC��OD��
��1����ͼ1����A��O��D������ͬһ��ֱ��������֤��S��AOC��S��BOD��
��2����ͼ2����A��O��D���㲻��ͬһ��ֱ��������OAB����OCD���ص�����S��AOC��S��BOD�Ƿ��Գ�������������������֤��������������Ҳ��˵��������
��3����A��O��D���㲻��ͬһ��ֱ��������OAB����OCD�в����ص���������ͼ��������ֱ��д�� S��AOC��S��BOD�Ĵ�С��ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
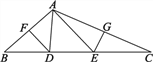
����Ŀ����ͼ����ABC�У���BAC��110�㣬AB�Ĵ�ֱƽ���߽�BC�ڵ�D��AC�Ĵ�ֱƽ���߽�BC�ڵ�E��BC��10cm.��
(1)��ADE���ܳ���
(2)��DAE�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
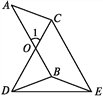
����Ŀ����ͼ,�߶�AB=CD,AB��CD�ཻ�ڵ�O,����1=60��,CE����ABƽ������,��ȷ��AC+BD��AB�Ĵ�С��ϵ,��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��ij�칫��¥��ǰ����һ���߶���15�����ED���Ӱ칫¥����A�����˶���E�ĸ��Ǧ���45�㣬��˵�D����¥ǰ�ݿ��ױߵľ���DC��20�ף��ݿ��³�BC��12�ף��ݿ��¶�i=1�� ![]() �����¥AB�ĸ߶��Ƕ��٣�����ȷ��0.1�ף��ο����ݣ�
�����¥AB�ĸ߶��Ƕ��٣�����ȷ��0.1�ף��ο����ݣ� ![]() ��1.41��
��1.41�� ![]() ��1.73��
��1.73�� ![]() ��2.45��
��2.45��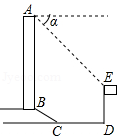
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ADΪ��ABC�Ľ�ƽ���ߣ�DE��AB�ڵ�E��DF��AC�ڵ�F������EF��AD�ڵ�G��

��1����֤��AD��ֱƽ��EF��
��2������BAC=60�����²�DG��AG���к�������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ĸ������ϵĵ�A����ʾʵ��a�����У�һ������|a|��|-2|�����Ϊ__________.




�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
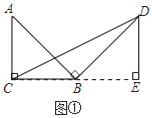
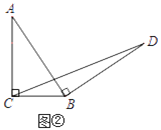
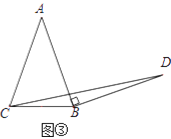
����Ŀ������ԭ�ͣ���ͼ�����ڵ���ֱ��������ABC�У���ACB=90����BC=a������AB�Ƶ�B˳ʱ����ת90���õ��߶�BD������CD������D����BCD��BC���ϵĸ�DE�� ��֤��ABC�ա�BDE���Ӷ��õ���BCD�����Ϊ![]() ��
��
����̽������ͼ������Rt��ABC�У���ACB=90����BC=a������AB�Ƶ�B˳ʱ����ת90���õ��߶�BD������CD���ú�a�Ĵ���ʽ��ʾ��BCD���������˵�����ɣ�
��Ӧ�ã���ͼ�����ڵ���������ABC�У�AB=AC��BC=a������AB�Ƶ�B˳ʱ����ת90���õ��߶�BD������CD��ֱ��д����BCD����������ú�a�Ĵ���ʽ��ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУʵ��ѧ��ʽ��ѧ����ӡ�����ɷݽ�ѧѧ��.ӡˢ���У��ס��������շѷ�ʽ������ӡ����ȡӡˢ���⣬���ַ�ʽ������ȡ�ư�Ѷ����ֲ���Ҫ������ӡˢ��ʽ�ķ���y��Ԫ����ӡˢ����x���ݣ�֮��Ĺ�ϵ��ͼ��ʾ.

��1����գ������շѷ�ʽ�ĺ�����ϵʽ��__________�������շѷ�ʽ�ĺ�����ϵʽ��__________.
��2����Уij�꼶ÿ����ӡ��100��450����100��450����ѧ����ѡ������ӡˢ��ʽ�Ϻ���.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com