
����Ŀ��Ϊ��һ���ƹ���������������μ���ij��ѧ���ѿ����Aʵ����B������Զ��C�ܲ���D�������ֻ��Ŀ��ѧ��ϲ��������е��飬�����ȡ�˲���ѧ�����������������Ƴ�ͼ1��ͼ2��ͳ��ͼ������ͼ�е���Ϣ����������⣺
��1������㱾�ε�����ϲ�����ܲ�����ѧ����������ռ�ٷֱȣ���������ͳ��ͼ����������
��2�������ȡ��5��ϲ�����ܲ�����ѧ����������3��Ů����2���������ִ���5��ѧ���������ȡ2��ѧ�������û���״ͼ���б��ķ���������պó鵽ͬ�Ա�ѧ���ĸ��ʣ�
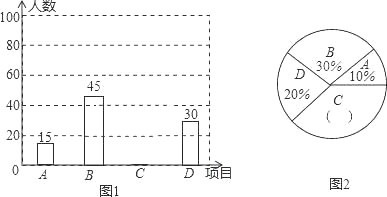
���𰸡�(1)60�ˣ�40%����2��
�������������������1����A������������ռ�İٷֱȣ�������������ѧ�������ó�����������ȥA��B��D�����������ϲ�����ܲ�����ѧ���������ٳ��Ա������ѧ�����������ռ�İٷֱȣ��ٻ�ͼ���ɣ�
��2����A��ʾ������B��ʾŮ������������ͼ���ٸ��ݸ��ʹ�ʽ���м��㼴�ɣ�
�����������1����������ã�
15��10%=150��������
���������ϲ�����ܲ�����ѧ�������ǣ�150-15-45-30=60���ˣ���
��ռ�ٷֱ��ǣ� ![]() ��100%=40%��
��100%=40%��
��ͼ���£�

��2����A��ʾ������B��ʾŮ������ͼ���£�

����20�������ͬ�Ա�ѧ���������8�֣�
��պó鵽ͬ�Ա�ѧ���ĸ�����![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�����߾���ԭ��O������ΪA��1��1��������ֱ��y=x��2����B��C���㣮
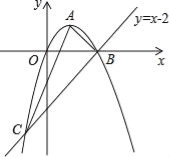
��1���������ߵĽ���ʽ����C�����ꣻ
��2����֤����ABC��ֱ�������Σ�
��3������NΪx���ϵ�һ�����㣬����N��MN��x���������߽��ڵ�M�����Ƿ������O��M��NΪ���������������ABC���ƣ������ڣ��������N�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1���۲���룺
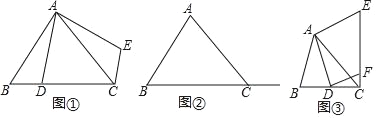
��Rt��ABC�У���BAC=90�㣬AB=AC����D�ڱ�BC�ϣ�����AD������ABD�Ƶ�A��ʱ����ת90������D���ڵ�E������ͼ����ʾ�����߶�CE���߶�BD��������ϵ���� ����λ�ù�ϵ���� ����
��2��̽��֤����
�ڣ�1���������£�����D���߶�BC���ӳ����ϣ����жϣ�1���н����ǻ�����������ͼ���л���ͼ�Σ���֤������жϣ�
��3����չ���죺
��ͼ�ۣ���BAC��90������AB��AC����ACB=45����AC=![]() �������������䣬����D��DF��AD��CE�ڵ�F����ֱ��д���߶�CF���ȵ����ֵ��
�������������䣬����D��DF��AD��CE�ڵ�F����ֱ��д���߶�CF���ȵ����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
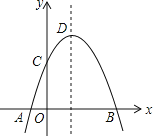
����Ŀ����ͼ��������y����x2��2x��m��1��x���ڵ�A(a��0)��B��b��0������y���ڵ�C�������ߵĶ���ΪD�������ĸ��жϣ��ٵ�x>0ʱ��y>0������a����1����b��4������������������P��x1��y1����Q��x2��y2������x1<1< x2����x1��x2>2����y1> y2���ܵ�C���������߶Գ���ĶԳƵ�ΪE����G��F�ֱ���x���y���ϣ���m��2ʱ���ı���EDFG�ܳ�����СֵΪ![]() ��������ȷ�жϵ�����ǣ� ��
��������ȷ�жϵ�����ǣ� ��
A. �� B. �� C. �� D. ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���߳�Ϊ 7 �������� OABC ������ƽ��ֱ������ϵ�У����� P �ӵ� C �������� ÿ�� 1 ����λ���ٶ��� O �˶����� Q �ӵ� O ͬʱ��������ÿ�� 1 ����λ���ٶ���� A �˶�������˵㼴ֹͣ�˶����˶�ʱ��Ϊ t �룬�� PQ��BP��BQ��
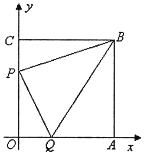
��1��д�� B ������ꣻ
��2��������
ʱ�� t����λ���룩 | 1 | 2 | 3 | 4 | 5 | 6 |
OP �ij��� | ||||||
OQ �ij��� | ||||||
PQ �ij��� | ||||||
�ı��� OPBQ ����� |
���������������ݣ��������߶� PQ �ij��ȵı仯���ɣ����²� PQ ���ȵ���Сֵ��
���������������ݣ������ı��� OPBQ ������Ƿ�ᷢ���仯����֤������۶ϣ�
��3����� M��N �ֱ��� BP��BQ ���е㣬д���� M��N �����꣬�Ƿ���ھ��� M�� N ����ķ�����������������ڣ���� t ��ֵ����������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB=3��BE��AC�ڵ�F������AD�ڵ�E������DF������EΪAD���е㣬��DF�ij�Ϊ__________ .
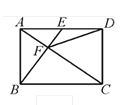
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijũ���а���ɽ����Ķ���ֹ���2000�ã�����ˮ���ܲ���Ϊ18000ǧ�ˣ���ˮ�����г���ÿǧ����![]() Ԫ���ڹ�ÿǧ����
Ԫ���ڹ�ÿǧ����![]() Ԫ
Ԫ![]() ����ũ����ˮ�������г�����ƽ��ÿ�����1000ǧ�ˣ���8�˰�æ��ÿ��ÿ�츶����25Ԫ��ũ�ó��˷Ѽ���������˰��ƽ��ÿ��100Ԫ��
����ũ����ˮ�������г�����ƽ��ÿ�����1000ǧ�ˣ���8�˰�æ��ÿ��ÿ�츶����25Ԫ��ũ�ó��˷Ѽ���������˰��ƽ��ÿ��100Ԫ��
��1���ֱ���![]() ��ʾ���ַ�ʽ����ˮ�������룮
��ʾ���ַ�ʽ����ˮ�������룮
��2����![]() Ԫ��
Ԫ��![]() Ԫ�������ַ�ʽ������ͬ��ʱ��������ȫ��ˮ��������ͨ������˵��ѡ�����ֳ��۷�ʽ�Ϻã�
Ԫ�������ַ�ʽ������ͬ��ʱ��������ȫ��ˮ��������ͨ������˵��ѡ�����ֳ��۷�ʽ�Ϻã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,һ�κ���y=kx+b��ͼ����A(8,0)��ֱ��y=-3x+6��x�ύ�ڵ�B,��y�ύ�ڵ�D,����ֱ�߽��ڵ�C(4,m).
(1)��m��ֵ��һ�κ����Ľ���ʽ��
(2)���ACD�������
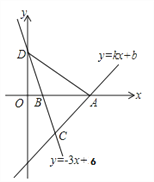
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com