



 解:将长方体沿AD,CD,EF,BF剪开,向左翻折,使面ADFE与面CDFB在同一个平面内,连接AB.(如图1)
解:将长方体沿AD,CD,EF,BF剪开,向左翻折,使面ADFE与面CDFB在同一个平面内,连接AB.(如图1) .
.

 <3
<3 <
<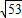 ,
, .
.




科目:初中数学 来源: 题型:
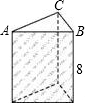 如图,是一个直三棱柱的模型,其底面是两直角边长分别为3cm、4cm的直角三角形,侧棱长都是8cm.
如图,是一个直三棱柱的模型,其底面是两直角边长分别为3cm、4cm的直角三角形,侧棱长都是8cm.查看答案和解析>>
科目:初中数学 来源: 题型:
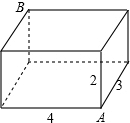 如图,是一个棱长分别为2、3、4的长方体,一只蜘蛛在顶点A处,一只小昆虫在顶点B处,则蜘蛛接近小昆虫时所爬行的最短路线的长是( )
如图,是一个棱长分别为2、3、4的长方体,一只蜘蛛在顶点A处,一只小昆虫在顶点B处,则蜘蛛接近小昆虫时所爬行的最短路线的长是( )A、
| ||
| B、7 | ||
C、
| ||
| D、6 |
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
 如图,是一个棱长分别为2、3、4的长方体,一只蜘蛛在顶点A处,一只小昆虫在顶点B处,则蜘蛛接近小昆虫时所爬行的最短路线的长是
如图,是一个棱长分别为2、3、4的长方体,一只蜘蛛在顶点A处,一只小昆虫在顶点B处,则蜘蛛接近小昆虫时所爬行的最短路线的长是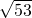
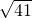
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
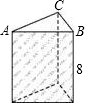 如图,是一个直三棱柱的模型,其底面是两直角边长分别为3cm、4cm的直角三角形,侧棱长都是8cm.
如图,是一个直三棱柱的模型,其底面是两直角边长分别为3cm、4cm的直角三角形,侧棱长都是8cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com