
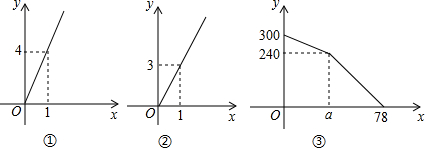
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据题意和函数图象可以分别判断出题目中给出的四个说法是否正确,从而可以解答本题.
解答 解:由图①可知,售票10分中,新增购票人数为:4×10=40(人),故(1)正确;
由图②可知每个售票窗口1分钟售票为3张,故a=(300-240)÷(2×3-4)=30,故(2)正确;
设过点(30,240),(78,0)的函数解析式为:y=kx+m
则$\left\{\begin{array}{l}{30k+m=240}\\{78k+m=0}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{k=-5}\\{m=390}\end{array}\right.$,
即y=-5x+390,
当y=90时,90=-5x+390,得x=60,故(3)正确;
由题意可得,240=[(2+b)×3-4]×(78-30)
解得,b=1,故(4)错误;
故选C.
点评 本题考查一次函数的应用,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,AD∥BC,∠C=90°,AB=AD=25,BC=32,连接BD,AE⊥BD,垂足为E.
如图,在四边形ABCD中,AD∥BC,∠C=90°,AB=AD=25,BC=32,连接BD,AE⊥BD,垂足为E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
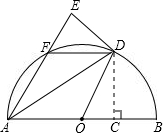 如图,AB是半圆O的直径,点C为半径OB上一点,过点C作CD⊥AB交半圆O于点D,将△ACD沿AD翻折得到△AED,AE交半圆O于点F,连接DF、OD.
如图,AB是半圆O的直径,点C为半径OB上一点,过点C作CD⊥AB交半圆O于点D,将△ACD沿AD翻折得到△AED,AE交半圆O于点F,连接DF、OD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
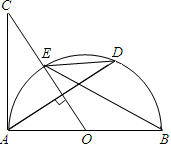 如图,AB是⊙O的直径,过圆心O作弦AD的垂线交半⊙O于点E,交AC于点C,使∠BED=∠C.
如图,AB是⊙O的直径,过圆心O作弦AD的垂线交半⊙O于点E,交AC于点C,使∠BED=∠C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com