练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，矩形OABC的两点OA、OC分别在x轴、y轴的正半轴上，点G为矩形对角线的交点，经过点G的双曲线y= 在第一象限的图象与BC相交于点M，交AB于N，若已知S△MBN=9，则k的值为 ．

    【答案】8
    【解析】解设点G的坐标（a，b），则B（2a，2b），
    ∴ab=k，
    ∵M点在矩形的边BC上，
    ∴点M的纵坐标=2b，
    ∵点M在双曲线y= 上，
    ∴M（ ，2b），同理N（2a， ），
    ∴BM=2a﹣ ，BN=2b﹣ ，
    ∵S△MBN=9，
    ∴ BMBN= （2a﹣ ）（2b﹣ ）= =9，
    ∴ab=k=8，
    ∴k=8．
    【考点精析】本题主要考查了矩形的性质的相关知识点，需要掌握矩形的四个角都是直角，矩形的对角线相等才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在菱形ABCD中，∠ABC=60°，E是对角线AC上任意一点，F是线段BC延长线上一点，且CF=AE，连接BE、EF．

    （1）如图1，当E是线段AC的中点，且AB=2时，求△ABC的面积；
    （2）如图2，当点E不是线段AC的中点时，求证：BE=EF；
    （3）如图3，当点E是线段AC延长线上的任意一点时，（2）中的结论是否成立？若成立，请给予证明；若不成立，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，O为原点，点A（﹣2，0），点B（0，2），点E，点F分别为OA，OB的中点．若正方形OEDF绕点O顺时针旋转，得正方形OE′D′F′，记旋转角为α．

    （1）如图①，当α=90°时，求AE′，BF′的长；
    （2）如图②，当α=135°时，求证AE′=BF′，且AE′⊥BF′；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

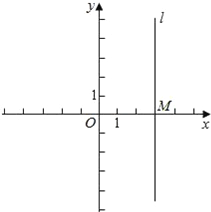
    【题目】在平面直角坐标系中，直线l过点M（3，0），且平行于y轴．

    （1）如果△ABC三个顶点的坐标分别是A（﹣2，0），B（﹣1，0），C（﹣1，2），△ABC关于y轴的对称图形是△A1B1C1，△A1B1C1关于直线l的对称图形是△A2B2C2，写出△A2B2C2的三个顶点的坐标；

    （2）如果点P的坐标是（﹣a，0），其中a＞0，点P关于y轴的对称点是P1，点P1关于直线l的对称点是P2，求PP2的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知在平面直角坐标系中有A(－2，1)，B(3，1)，C(2，3)三点．请回答下列问题：

    (1)在坐标系内描出点A，B，C的位置．

    (2)求出以A，B，C三点为顶点的三角形的面积．

    (3)在y轴上是否存在点P，使以A，B，P三点为顶点的三角形的面积为10？若存在，请直接写出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在一次暑假旅游中，小亮在仙岛湖的游船上（A处），测得湖西岸的山峰太婆尖（C处）和湖东岸的山峰老君岭（D处）的仰角都是45°．游船向东航行100米后（B处），测得太婆尖，老君岭的仰角分别为30°，60°．试问太婆尖、老君岭的高度为多少米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知抛物线y=ax2+bx+c（a≠0）经过A（﹣1，0），B（4，0），C（0，2）三点．

    （1）求这条抛物线的解析式；
    （2）E为抛物线上一动点，是否存在点E，使以A、B、E为顶点的三角形与△COB相似？若存在，试求出点E的坐标；若不存在，请说明理由；
    （3）若将直线BC平移，使其经过点A，且与抛物线相交于点D，连接BD，试求出∠BDA的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知△ABD和△AEC中，AD=AB，AE=AC，∠DAB=∠EAC=60°，CD、 BE相交于点P．

    （1）用全等三角形判定方法证明：BE＝DC

    （2）求∠BPC的度数；

    （3）在（2）的基础上，经过深入探究后发现：射线AP平分∠BPC，请判断你的发现是否正确，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC由△A′B′C′绕O点旋转180°而得到，则下列结论不成立的是（ ）

    A.点A与点A′是对应点
    B.BO=B′O
    C.∠ACB=∠C′A′B′
    D.AB∥A′B′

    查看答案和解析>>

    同步练习册答案