练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．计算（-3）0的结果为（　　）
    A．0B．1C．-3D．3

    分析 直接利用零指数幂的性质化简求出答案．

    解答 解：（-3）0=1．
    故选：B．

    点评 此题主要考查了零指数幂的性质，正确把握定义是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    7．一个圆形转盘被平均分成红、黄、蓝3个扇形区域，向其投掷一枚飞镖，飞镖落在转盘上，则飞镖落在黄色区域的概率是$\frac{1}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

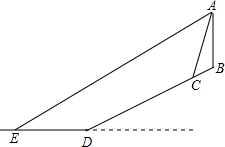    15．中考结束后，小明和好朋友一起前往三亚旅游．他们租住的宾馆AB坐落在坡度为i=1：2.4的斜坡上．某天，小明在宾馆顶楼的海景房A处向外看风景，发现宾馆前的 一座雕像C的俯角为76°（雕像的高度忽略不计），远处海面上一艘即将靠岸的轮船E的俯角为27°．已知雕像C距离海岸线D的距离CD为260米，与宾馆AB的水平距离为36米，问此时轮船E距离海岸线D的距离ED的长为（　　）（参考数据：tan76°≈4.0，tan27°≈0.5，sin76°≈0.97，sin27°≈0.45．
    A．262B．212C．244D．276

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．点P（m-1，2m+1）在第二象限，则m的取值范围是（　　）
    A．$m＞\frac{1}{2}$B．m＜1C．$m＜-\frac{1}{2}$或m＞1D．$-\frac{1}{2}＜m＜1$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．先阅读理解下面的例题，再按要求解答下列问题：
    例题：求代数式y2+4y+8的最小值．
    解：y2+4y+8=y2+4y+4+4=（y+2）2+4
    ∵（y+2）2≥0
    ∴（y+2）2+4≥4
    ∴y2+4y+8的最小值是4．
    （1）求代数式（x-1）2+5的最小值；
    （2）求代数式m2+2m+4的最小值；
    （3）某居民小区要在一块一边靠墙（墙长15m）的空地上建一个长方形花园ABCD，花园一边靠墙，另三边用总长为20m的栅栏围成．如图，设AB=x（m），请问：当x取何值时，花园的面积最大？最大面积是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．如图1，在菱形ABCD中，AC=2，BD=2$\sqrt{3}$，AC，BD相交于点O．

    （1）求边AB的长；
    （2）如图2，将一个足够大的直角三角板60°角的顶点放在菱形ABCD的顶点A处，绕点A左右旋转，其中三角板60°角的两边分别与边BC，CD相交于点E，F，连接EF，判断△AEF是哪一种特殊三角形，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．矩形ABCD和矩形CEFG的长与宽之比AB：BC=$\sqrt{3}$：1，且AC=CE．（注：直角三角形中，如果一条直角边等于斜边的一半，那么这条直角边所对的锐角是30°）

    （1）如图（1），当B，C，E在同一条直线上，点D在CG上，且BC=2时，连接AF，求线段AF的长．
    （2）在图（1）中取AF的中点M，并连接BM，EM得到图（2），求证：△BEM是等边三角形；
    （3）如果将图（2）中的矩形ABCD绕点C旋转一定角度得到图（3），试问：△BEM是等边三角形三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．某村引进甲乙两种水稻良种，各选6块条件相同的实验田，同时播种并核定亩产，结果甲、乙两种水稻的平均产量均为550kg/亩．方差分别为${{S}_{甲}}^{2}$=141.7，${{S}_{乙}}^{2}$=433.3，则产量稳定，适合推广的品种为甲．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．某商场连续5个月统计了A、B两种品牌冰箱的销售情况（单位：台）．
    A品牌：15，16，17，13，14
    B品牌：10，14，15，20，16
    （1）求出A品牌冰箱数据的方差；
    （2）已知B品牌冰箱月销售量的平均数为$\overline{{x}_{B}}$=15，方差为SB2=10.4，你认为这两种品牌冰箱哪一种的月销量比较稳定？

    查看答案和解析>>

    同步练习册答案