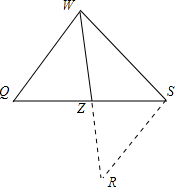
解:过S作SR∥WQ交WZ的延长线于R,
∴∠R=∠QWZ,
∵WZ平分∠QWS,
∴∠QWZ=∠SWZ,
∴∠R=∠SWZ,
∴WS=SR,
∵SR∥WQ,
∴
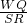
=
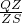
,
∴
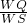
=
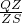
,
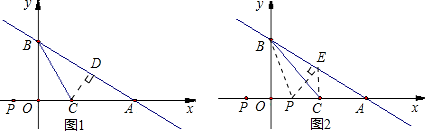
(1)解:当x=0时,y=3,
当y=0时,x=4,
∴A(4,0),B(0,3),
∵当P点运动到与原点O重合时,P点关于直线BC的对称点恰好落在直线AB上,
∴

=
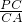
,
即:

=
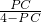
,
解得:PC=

,
答:PC的长是

.
(2)解:设OP=x,
∴
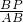
=
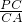
,
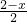
=
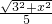
,
解得:x
1=4,x
2=

,
经检验x=4不是原方程的解,舍去,
答:P点运动到OP=

时,点P关于直线BC的对称点落在直线AB上.
分析:过S作SR∥WQ交WZ的延长线于R,由平行得到∠QWZ=∠SWZ和
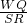
=
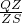
,根据等腰三角形的判定和性质得出WS=SR和
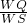
=
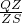
;
(1)把x=0和y=0代入求出A、B的坐标,根据勾股定理求出AB,根据上式得出的规律得出

=
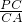
,代入即可求出PC;
(2)设OP=x,根据上式得出的规律得到
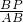
=
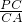
,代入得出方程
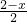
=
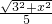
,求出即可.
点评:本题主要考查对一次函数图象上点的坐标特征,勾股定理,等腰三角形的性质和判定,平行线的性质平行线分线段成比例定理,三角形的角平分线等知识点的理解和掌握,综合运用这些性质进行计算是解此题的关键.题型较好,难度适中.

 x+3与x轴、y轴交于A、B两点,C点为线段AO上一点,一动点P在x轴上.
x+3与x轴、y轴交于A、B两点,C点为线段AO上一点,一动点P在x轴上.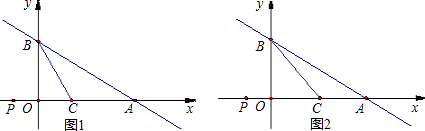
 解:过S作SR∥WQ交WZ的延长线于R,
解:过S作SR∥WQ交WZ的延长线于R,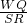 =
=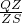 ,
,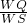 =
=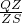 ,
,
 =
=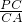 ,
, =
=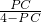 ,
, ,
, .
.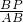 =
=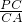 ,
,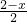 =
=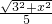 ,
, ,
, 时,点P关于直线BC的对称点落在直线AB上.
时,点P关于直线BC的对称点落在直线AB上.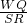 =
=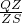 ,根据等腰三角形的判定和性质得出WS=SR和
,根据等腰三角形的判定和性质得出WS=SR和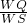 =
=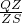 ;
; =
=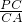 ,代入即可求出PC;
,代入即可求出PC;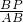 =
=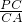 ,代入得出方程
,代入得出方程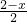 =
=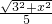 ,求出即可.
,求出即可.

 12、已知如图直线l1∥l2,直线l3分别和l1、l2相交于A、B.求证∠1=∠3.(请在下列横线上填上合适的理由).例:证明:因为l1∥l2
12、已知如图直线l1∥l2,直线l3分别和l1、l2相交于A、B.求证∠1=∠3.(请在下列横线上填上合适的理由).例:证明:因为l1∥l2 如图直线l1、l2上所有点的坐标分别是关于x,y的方程y=2x+b,y=ax+3的解,则方程组
如图直线l1、l2上所有点的坐标分别是关于x,y的方程y=2x+b,y=ax+3的解,则方程组