练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．某商场有一批进价为12元的商品A，当定价为20元时，每天可以售出240个，根据市场调查发现，在定价20元的基础上，该商品：
    （1）每个涨价1元，则每天少售出20个，（2）每个降价1元，则每天多售出40个，
    为了使商品A每天获得利润1920元，定价应为多少元？

    分析 设定价为x元，则有（x-进价）[每天售出的数量-（x-20）×20]=每天利润；解方程求解即可．

    解答 解：当涨价时，设每件商品定价为x元，则每件商品的销售利润为（x-12）元，
    根据题意，得
    [240-20（x-20）]×（x-12）=1920
    整理，得x2-44x+480=0
    解得，x1=20，x2=24
    当降价时，设每件商品定价为y元，则每件商品的销售利润为（y-12）元，
    根据题意，得[240+40（20-y）]×（y-12）=1920
    整理，得y2-38y+360=0
    解得，y1=20，y2=18，
    综上所述，比较两种方案后，定价为18元更合理．

    点评 本题考查的是一元二次方程的应用．读懂题意，找到等量关系“要使商品每天获利1920元”准确的列出方程是解题的关键

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    17．计算：
    （1）$\sqrt{3}$+$\sqrt{12}$-3$\sqrt{18}$+7$\sqrt{2}$．
    （2）3$\sqrt{18}$×$\frac{1}{6}$$\sqrt{3}$÷2$\sqrt{6}$
    （3）$\frac{6}{{\sqrt{3}}}$-$\frac{2}{{\sqrt{3}-1}}$．
    （4）8$\sqrt{{a^2}b}$÷2$\sqrt{ab}$×$\sqrt{\frac{a}{b}}$（a＞0）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．已知抛物线y=$\frac{1}{8}$x2-$\frac{1}{4}$x-1与x轴交于A、B两点（点A在点B的左侧）与y轴交于点C
    （1）求抛物线与坐标轴的交点坐标；
    （2）求△ABC外接圆的圆心Q的坐标；
    （3）在抛物线的对称轴上一定存在点P，使得∠APB=∠ACB，直接写出点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．若实数x，y满足（x-$\sqrt{{x}^{2}-2016}$）（y-$\sqrt{{y}^{2}-2016}$）=2016．
    （1）求x，y之间的数量关系；
    （2）求3x2-2y2+3x-3y-2017的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．18-6÷（-2）×（+$\frac{1}{3}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

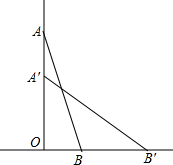    12．如图，一个长为15m的梯子斜靠在墙上，梯子的顶端距地面的距离为12m，
    ①如果梯子的顶端下滑了1m，那么梯子的底端也向后滑动1m吗？请通过计算解答．
    ②梯子的顶端从A处沿墙AO下滑的距离与点B向外移动的距离有可能相等吗？若有可能，请求出这个距离，没有可能请说明理由．
    ③若将上题中的梯子换成15米长的直木棒，将木棒紧靠墙竖直放置然后开始下滑改至直木棒的顶端A滑至墙角O处，试求出木棒的中点Q滑动的路径长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．先化简，再求值：[（x-2y）（x+2y）+4（x-y）2]÷2x，其中：x=-2，y=-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．如图，在△ABC中，BD，CE是两条高，点O为BC的中点，连接OD，OE，
    求证：B，C，D，E四个点在以点O为圆心的同一个圆上．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．已知9+$\sqrt{13}$与9-$\sqrt{13}$的小数部分分别是a和b，求ab-4a+3b-12的值．

    查看答案和解析>>

    同步练习册答案