Question

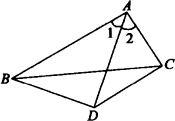
如图所示，△ABC中，AB＝2AC，∠1＝∠2，DA＝DB，你能用两种或两种以上的方法证明DC⊥AC吗？

Answer 1

答案：
解析：
提示：

遇有等腰三角形的有关题目，常常利用等腰三角形“三线合一”的性质来添加辅助线，或者作等腰三角形底边的高(中线或顶角的平分线)，或者以某线段为底边上的高(中线或顶角的平分线)作等腰三角形． 　　证法一欲证AC⊥DC，只需说明∠ACD＝90°，由于DA＝DB，故想到作DE⊥AB，构造直角∠AED，只要说明∠ACD＝∠AED．本题就得解，从而只需说明△AED≌△ACD． 　　证法二欲证AC⊥DC，可以考虑说明DC或AC为某个等腰三角形底边上的高，由已知AB＝2AC，就确定了DC为高，故延长AC至E点，连结DE，只要说明AD＝DE．本题就可解答．由DA＝DB可知，需要说明DE＝DB，从而需要说明△ADB≌△ADE由AB＝AC，∠1＝∠2，AD＝AD，可顺利解答本题