
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,其对称轴交抛物线于点
,其对称轴交抛物线于点![]() ,交
,交![]() 轴于点
轴于点![]() ,已知
,已知![]() .
.
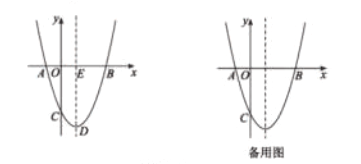
⑴求抛物线的解析式及点![]() 的坐标;
的坐标;
⑵连接![]() 为抛物线上一动点,当
为抛物线上一动点,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
⑶平行于![]() 轴的直线交抛物线于
轴的直线交抛物线于![]() 两点,以线段
两点,以线段![]() 为对角线作菱形
为对角线作菱形![]() ,当点
,当点![]() 在
在![]() 轴上,且
轴上,且![]() 时,求菱形对角线
时,求菱形对角线![]() 的长.
的长.
【答案】(1)y=![]() x2﹣2x﹣6,D(2,﹣8);(2)F点的坐标为(7,
x2﹣2x﹣6,D(2,﹣8);(2)F点的坐标为(7,![]() )或(5,﹣
)或(5,﹣![]() );(3)菱形对角线MN的长为
);(3)菱形对角线MN的长为![]() +1或
+1或![]() ﹣1.
﹣1.
【解析】试题分析:(1)由条件可求得B、C坐标,利用待定系数法可求得抛物线解析式,进一步可求得D点坐标;(2)过F作FG⊥x轴于点G,可设出F点坐标,利用△FAG∽△BDE,由相似三角形的性质可得到关于F点坐标的方程,可求得F点的坐标;(3)可求得P点坐标,设T为菱形对角线的交点,设出PT的长为n,从而可表示出M点的坐标,代入抛物线解析式可得到n的方程,可求得n的值,从而可求得MN的长.
试题解析:
(1)∵OB=OC=6,
∴B(6,0),C(0,﹣6),
∴ ,解得
,解得![]() ,
,
∴抛物线解析式为y=![]() x2﹣2x﹣6,
x2﹣2x﹣6,
∵y=![]() x2﹣2x﹣6=
x2﹣2x﹣6=![]() (x﹣2)2﹣8,
(x﹣2)2﹣8,
∴点D的坐标为(2,﹣8);
(2)如图1,过F作FG⊥x轴于点G,
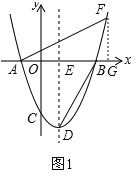
设F(x,![]() x2﹣2x﹣6),则FG=|
x2﹣2x﹣6),则FG=|![]() x2﹣2x﹣6|,
x2﹣2x﹣6|,
在y=![]() x2﹣2x﹣6中,令y=0可得
x2﹣2x﹣6中,令y=0可得![]() x2﹣2x﹣6=0,解得x=﹣2或x=6,
x2﹣2x﹣6=0,解得x=﹣2或x=6,
∴A(﹣2,0),
∴OA=2,则AG=x+2,
∵B(6,0),D(2,﹣8),
∴BE=6﹣2=4,DE=8,
当∠FAB=∠EDB时,且∠FGA=∠BED,
∴△FAG∽△BDE,
∴![]() ,即
,即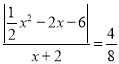 =
=![]() ,
,
当点F在x轴上方时,则有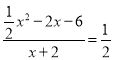 ,解得x=﹣2(舍去)或x=7,此进F点坐标为(7,
,解得x=﹣2(舍去)或x=7,此进F点坐标为(7,![]() );
);
当点F在x轴上方时,则有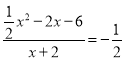 ,得x=﹣2(舍去)或x=5,此进F点坐标为(5,﹣
,得x=﹣2(舍去)或x=5,此进F点坐标为(5,﹣![]() );
);
综上可知F点的坐标为(7,![]() )或(5,﹣
)或(5,﹣![]() );
);
(3)∵点P在x轴上,
∴由菱形的对称性可知P(2,0),
如图2,当MN在x轴上方时,设T为菱形对角线的交点,
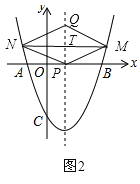
∵PQ=![]() MN,
MN,
∴MT=2PT,
设PT=n,则MT=2n,
∴M(2+2n,n),
∵M在抛物线上,
∴n=![]() (2+2n)2﹣2(2+2n)﹣6,解得n=
(2+2n)2﹣2(2+2n)﹣6,解得n=![]() 或n=
或n=![]() ,
,
∴MN=2MT=4n=![]() +1;
+1;
当MN在x轴下方时,同理可设PT=n,则M(2+2n,﹣n),
∴﹣n=![]() (2+2n)2﹣2(2+2n)﹣6,解得n=
(2+2n)2﹣2(2+2n)﹣6,解得n=![]() 或n=
或n=![]() (舍去),
(舍去),
∴MN=2MT=4n=![]() ﹣1;
﹣1;
综上可知菱形对角线MN的长为![]() +1或
+1或![]() ﹣1.
﹣1.


 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案科目:初中数学 来源: 题型:
【题目】某公司为奖励在趣味运动会上取得好成绩的员工,计划购买甲、乙两种奖品共20件,其中甲种奖品每件40元,乙种奖品每件30元.
(1)如果购买甲、乙两种奖品共花费了650元,求甲、乙两种奖品各购买了多少件;
(2)如果购买乙种奖品的件数不超过甲种奖品件数的2倍,总花费不超过680元,求该公司有哪几种不同的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() 在抛物线
在抛物线![]() 上.
上.
(1)求抛物线的解析式;
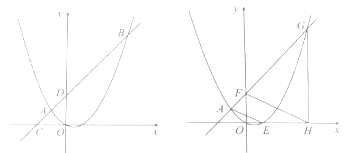
(2)如图1,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 交抛物线于另一点
交抛物线于另一点![]() ,过点
,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,设抛物线与
,设抛物线与![]() 轴的正半轴交于点
轴的正半轴交于点![]() ,连接
,连接![]() ,求证
,求证![]() ;
;
(3)如图2,直线![]() 分别交
分别交![]() 轴,
轴,![]() 轴于
轴于![]() 两点,点
两点,点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 方向匀速运动,速度为每秒
方向匀速运动,速度为每秒![]() 个单位长度,同时点
个单位长度,同时点![]() 从原点
从原点![]() 出发,沿
出发,沿![]() 轴正方向匀速运动,速度为每秒1个单位长度,点
轴正方向匀速运动,速度为每秒1个单位长度,点![]() 是直线
是直线![]() 与抛物线的一个交点,当运动到
与抛物线的一个交点,当运动到![]() 秒时,
秒时,![]() ,直接写出
,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将9.52变形正确的是( )
A. 9.52=92+0.52 B. 9.52=(10+0.5)(10﹣0.5)
C. 9.52=102﹣2×10×0.5+0.52 D. 9.52=92+9×0.5+0.52
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,CD是中线,AC=BC,一个以点D为顶点的45°角绕点D旋转,使角的两边分别与AC、BC的延长线相交,交点分别为点E,F,DF与AC交于点M,DE与BC交于点N.
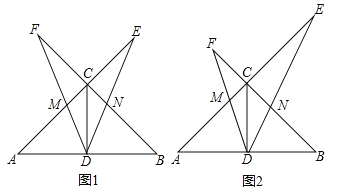
(1)如图1,若CE=CF,求证:DE=DF;
(2)如图2,在∠EDF绕点D旋转的过程中:
①探究三条线段AB,CE,CF之间的数量关系,并说明理由;
②若CE=4,CF=2,求DN的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com