
【题目】已知直线y=kx+b经过点A(﹣3,﹣8),且与直线![]() 的公共点B的横坐标为6.
的公共点B的横坐标为6.
(1)求直线y=kx+b的表达式;
(2)设直线y=kx+b与y轴的公共点为点C,求△BOC的面积.
【答案】(1)![]() (2)12.
(2)12.
【解析】(1)先由已知直线求得点B的坐标,再根据待定系数法求得直线y=kx+b的表达式;
(2)先根据求得的直线解析式,求得点C的坐标,再根据点C和点B的位置,计算△BOC的面积.
解:(1)在直线![]() 中,由 x=6,得
中,由 x=6,得![]() ,
,
∴点B(6,4),
由直线y=kx+b经过点A、B,得
![]() ,解得
,解得 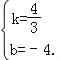
∴所求直线表达式为![]() ;
;
(2)在直线![]() 中,当 x=0时,得 y=﹣4,
中,当 x=0时,得 y=﹣4,
即C(0,﹣4),
由点B(6,4)、C(0,﹣4),可得
△BOC的面积=![]()
![]() ×4×6=12,
×4×6=12,
∴△BOC的面积为12.
“点睛”本题主要考查了两直线相交或平行的问题,解决问题的关键是掌握待定系数法求一次函数解析式,解题时注意:求一次函数y=kx+b,则需要两组x,y的值.


 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
【题目】下列各式中,正确的是( )
A. 2a+5b=7ab B. 4+5x=9x C. -3(x2-4)=-3x2+4 D. 2-3x=-(3x-2)
查看答案和解析>>
科目:初中数学 来源: 题型:
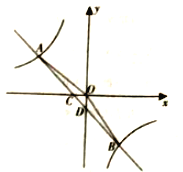
【题目】(2016重庆市第22题)如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于第二、四象限内的A,B两点,与x轴交于点C,与Y轴交于点D,点B的坐标为(m,-4),连接AO,AO=5,sin∠AOC=![]() 。
。
(1)求反比例函数的解析式;
(2)连接OB,求△AOB的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,AB=8,AD=4.点Q与点P同时从点A出发,点Q以每秒1个单位的速度沿A→D→C→B的方向运动,点P以每秒3个单位的速度沿A→B→C→D的方向运动,当P,Q两点相遇时,它们同时停止运动.设Q点运动的时间为x(秒),在整个运动过程中,当△APQ为直角三角形时,则相应的x的值或取值范围是_______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小虫从某点O出发,在一条直线上来回爬行,假定向右爬行的路程记为正数,向左爬行的路程记为负数,爬过的各段路程(单位: ![]() )依次为:+5、–3、+10、–8、–6、+12、–10.
)依次为:+5、–3、+10、–8、–6、+12、–10.
(1)小虫是否回到原点O?请说明理由;
(2)小虫离开出发点O最远是多少厘米?
(3)在爬行过程中每爬行![]() cm奖励两粒芝麻,那么小虫一共能得到多少粒芝麻?
cm奖励两粒芝麻,那么小虫一共能得到多少粒芝麻?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com