
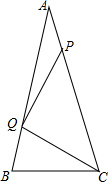
 如图所示,在△ABC中,AB=AC,∠BAC=30°,P、Q分别为AB、AC的点,且∠QPC=45°,PQ=BC,证明:BC=CQ.
如图所示,在△ABC中,AB=AC,∠BAC=30°,P、Q分别为AB、AC的点,且∠QPC=45°,PQ=BC,证明:BC=CQ. 分析 以BC为边,在△ABC内构造等边三角形DBC,连接DA、DP、DQ,得平行四边形BDPQ,利用平行四边形的性质说明PQ=DB=BC.
解答  证明:在△ABC内部做等边三角形DBC,连接DQ,DP,AD
证明:在△ABC内部做等边三角形DBC,连接DQ,DP,AD
∵△ABC中,AB=AC,∠BAC=30°
∴∠ABC=∠ACB=75°
∵等边三角形DBC中
∴BC=DB=DC
∴∠DBC=∠DCB=60°
∴∠ABD=∠ACD=15°
在△ABD与△ACD中
$\left\{\begin{array}{l}{AB=AC}\\{AD=AD}\\{BD=CD}\end{array}\right.$
∴△ABD≌△ACD(SAS)
∴∠BAD=∠CAD=15°
∴∠DBA=∠BAD,∠DAC=∠DCA
∴BD=AD=CD
∵∠BAC=30°,∠QPC=45°
∴∠AQP=∠QPC-∠BAC=15°
∴∠AQP=∠ABD
∴PQ∥BD
∵PQ=BC
∴PQ∥BD,PQ=BD
∴四边形BDPQ是平行四边形(一组对边平行且相等的四边形是平行四边形)
∴BQ=DP,BQ∥DP(平行四边形两组对边分别相等且平行)
∴∠QPD=∠ABD=15°(平行四边形对角相等)
∴∠DPC=30°
∴∠DPC=∠PAQ=30°,∠DCP=∠PQA=15°
∴CD=QP
在△DPC与△PAQ中
$\left\{\begin{array}{l}{∠DCP=∠PQA}\\{∠DPC=∠PAQ}\\{CD=QP}\end{array}\right.$
∴△DPC≌△PAQ(AAS)
∴DP=AP
在梯形AQDP中,AQ∥DP,PQ=BD=AD
∴DQ=AP(对角线相等的梯形是等腰梯形)
∴DP=DQ
∴BQ=DQ
在△BCQ与△DCQ中
$\left\{\begin{array}{l}{QC=QC}\\{BC=DC}\\{BQ=DQ}\end{array}\right.$
∴△BCQ≌△DCQ(SSS)
∴∠BCQ=∠DCQ=30°
∵△BCQ中,∠DCQ=30°,∠CBQ=75°
∴∠CQB=75°=∠CBQ
∴BC=CQ
点评 本题考查了等腰三角形、等边三角形、以及平行四边形的性质.做等边三角形构造平行四边形是关键.另本题的解决亦可运用反证法或者统一法.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
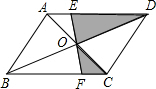 如图,?ABCD的面积是8,对角线AC、DB交于点O,EF过点O分别交AD、BC于E、F,则阴影部分的面积是( )
如图,?ABCD的面积是8,对角线AC、DB交于点O,EF过点O分别交AD、BC于E、F,则阴影部分的面积是( )| A. | 4 | B. | 2 | C. | 6 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 第50行第50列 | B. | 第50行第51列 | C. | 第51行第50列 | D. | 第51行第51列 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图△ABC为等腰直角三角形,其中∠A=90°,AB=AC=2,点D为BC中点,将一含45°角的三角板的一个锐角顶点落在点D处,三角板绕点D旋转,三角板两边分别与AB边与AC边交于点E、F两点.
如图△ABC为等腰直角三角形,其中∠A=90°,AB=AC=2,点D为BC中点,将一含45°角的三角板的一个锐角顶点落在点D处,三角板绕点D旋转,三角板两边分别与AB边与AC边交于点E、F两点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x+1)(x-1)=x2-1 | B. | a2-b2=(a+b)(a-b) | ||
| C. | x2-2x+1=x(x-2)+1 | D. | mx+my+nx+ny=m(x+y)+n(x+y) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com