练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知D、C为AE上的点，AD=CE，∠A=∠E，BC∥FD．求证：AB=EF．

    证明：∵AD=CE，
    ∴AD+DC=CE+DC即AC=ED．
    ∵BC∥FD，
    ∴∠ACB=∠EDF．
    在△ABC和△EFD中，
    ∵，
    ∴△ABC≌△EFD（ASA）．
    ∴AB=EF．
    分析：由已知条件先根据ASA判定△ABC≌△EFD，从而由三角形全等的性质求得AB=EF．
    点评：主要考查全等三角形的判定，常用的判定方法有AAS，SSS，SAS，HL等．由平行线得到角相等是正确解答本题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    精英家教网如图，已知E、F分别为矩形ABCD的边BA、DC的延长线上的点，且AE=
    1
    2
    AB，CF=
    1
    2
    CD，连接EF分别交AD、BC于点G、H．请你找出图中与DG相等的线段，并加以证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    精英家教网（任选一题做）
    （1）小明在一次实践活动课中，要对水管的外部进行包扎，包扎时用带子缠绕在管道外部．若要使带子全部包住管道且不重叠（不考虑管道两端的情况），需计算带子的缠绕角度α（α指缠绕中将部分带子拉成图中所示的平面ABCD时的∠ABC，其中AB为管道侧面母线的一部分）．若带子宽度为1，水管直径为2，则α的余弦值为
     
    ．



    （2）如图，已知AD是等腰△ABC底边上的高，且tan∠B=
    34
    ，AC上有一点E，满足AE：CE=2：3，则tan∠ADE的值是
     
    ．
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    23、已知D、C为AE上的点，AD=CE，∠A=∠E，BC∥FD．求证：AB=EF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

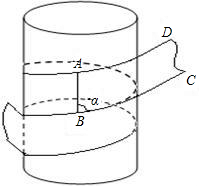
    （1）小明在一次实践活动课中，要对水管的外部进行包扎，包扎时用带子缠绕在管道外部．若要使带子全部包住管道且不重叠（不考虑管道两端的情况），需计算带子的缠绕角度α（α指缠绕中将部分带子拉成图中所示的平面ABCD时的∠ABC，其中AB为管道侧面母线的一部分）．若带子宽度为1，水管直径为2，则α的余弦值为______．



    （2）如图，已知AD是等腰△ABC底边上的高，且tan∠B=数学公式，AC上有一点E，满足AE：CE=2：3，则tan∠ADE的值是______．

    查看答案和解析>>

    同步练习册答案