练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．已知a、b、c是三角形的三边长，如果满足（a-5）2+|b-12|+c2-26c+169=0，则三角形的形状是（　　）
    A．底与边不相等的等腰三角形B．等边三角形
    C．钝角三角形D．直角三角形

    分析 根据给出的条件求出三角形的三边长，再根据勾股定理的逆定理来判定三角形的形状．

    解答 解：∵（a-5）2+|b-12|+c2-26c+169=0，
    ∴（a-5）2+|b-12|+（c-13）2=0，
    ∴a=5，b=12，c=13，
    ∵52+122=132，
    ∴此三角形是直角三角形．
    故选D．

    点评 本题考查了勾股定理的逆定理，用到的知识点是绝对值、偶次方的性质、勾股定理的逆定理、完全平方公式，关键是证出a，b，c之间的关系．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    14．若$\root{3}{{x}^{2}}$=x2，则x的值为0，±1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．下列各组的公因式是代数式x-2的是（　　）
    A．（x+2）2，（x-2）2B．x-2x，4x-6C．3x-6，x2-2xD．x-4，6x-18

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．已知函数y=x+b的图象与坐标轴围成的三角形面积为1，则b=（　　）
    A．±$\sqrt{2}$B．±2C．2D．$\sqrt{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．在平面直角坐标系xOy（如图）中，已知点A的坐标为（3，1），点B的坐标为（6，5），点C的坐标为（0，5）；某二次函数的图象经过点A、点B与点C．
    （1）求这个二次函数的解析式；
    （2）假如点Q在该函数图象的对称轴上，且△ACQ是等腰三角形，直接写出点Q的坐标；
    （3）如果第一象限内的点P在（1）中求出的二次函数的图象上，且tan∠PCA=$\frac{1}{2}$，求∠PCB的正弦值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

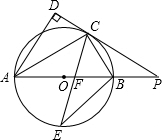    9．如图，AB是⊙O的直径，点C是⊙O上一点，AD和过点C的切线互相垂直，垂足为D，直线DC与AB的延长线相交于P．弦CE平分∠ACB，交直径AB于点F，连结BE．
    （1）求证：AC平分∠DAB；
    （2）探究线段PC，PF之间的大小关系，并加以证明；
    （3）若tan∠CEB=$\frac{3}{4}$，BE=5$\sqrt{2}$，求AC、BC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．计算：
    （1）计算：（-1）2017+2cos45°-$\frac{1}{2}$$\sqrt{8}$
    （2）化简：$\frac{{{m^2}-4}}{2m-2}$÷（1-$\frac{1}{m-1}$）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．某笔直河道上有甲、乙两港，相距120千米，一艘轮船从甲港出发，顺流航行4小时到达乙港，休息1小时后立即返回；一艘快艇在轮船出发3小时后从乙港出发，逆流航行3小时到达甲港，并立即返回（掉头时间忽略不计）．已知水流速度是5千米/时，下图表示轮船和快艇距甲港的距离y（千米）与轮船行驶时间x（小时）之间的函数关系，结合图象解答下列问题：（顺流速度=船在静水中速度+水流速度；逆流速度=船在静水中速度-水流速度）
    （1）轮船在静水中的速度是25千米/时；快艇在静水中的速度是45千米/时；
    （2）求线段DF的函数解析式，并写出自变量x的取值范围；
    （3）快艇出发多长时间，轮船和快艇在途中相距20千米？（直接写出结果）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

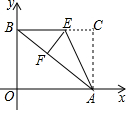    14．如图，已知AOBC是一张放在平面直角坐标系中的长方形纸片，O为原点，点A在x轴的正半轴上，点B在y轴的正半轴上，点C的坐标为（8，6），在BC边上取一点E，将纸片沿AE翻折，使点C恰好落在AB边上的点F处．
    （1）求AB的长；
    （2）求点E的坐标；
    （3）写出点F的坐标．

    查看答案和解析>>

    同步练习册答案