“百诚”公司投资750万元,成功研制出一种市场需求量较大的产品,并再投入资金1750万元进行相关生产设备的购买.已知生产过程中,每件产品的成本为60元.在销售过程中发现,当销售单价定为120元时,年销售量为24万件;销售单价每增加10元,年销售量将减少1万件.设销售单价为x(元)(x>120),年销售量为y(万件),第一年年获利(年获利=年销售额-生产成本-投资)为z(万元).
(1)请直接写出y与x之间,z与x之间的函数关系式:
______,______;
(2)计算销售单价为200元时的第一年年获利,请问公司此时亏损还是盈利?并说明为了得到同样的年获利,销售单价还可以定为多少元?
(3)公司计划:在第一年按年获利最大时确定的销售单价进行销售;第二年后总获利要不低于1840万元.请说明,第二年的销售单价x应确定在什么范围内.
【答案】
分析:(1)由题意根据单价之间的关系,销售单价每增加10元,年销售量将减少1万件,年获利=年销售额-生产成本-投资,列出y与x,z与x的函数关系式;(2)把x=200代入函数式求出z;(3)在第一年按年获利最大时确定的销售单价进行销售,根据z与x的关系式,配方求出最值;第二年后总获利要不低于1840万元,令z≤1840解出x值的范围.
解答:解:由题意得:
(1)y=24-
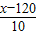
,即:
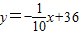
,
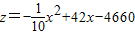
;
(2)当x取200时,
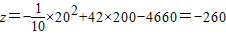
此时公司亏损了260万元
因为此抛物线的对称轴为x=210
所以当x=220时,也能获得同样的年获利
(3)
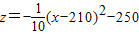
∴当x=210时,z取最大值,最大值为-250,
也就是说:当销售单价定为210元时,年获利最大,并且到第一年年底公司还差250万元就可收回全部投资
第二年的销售单价定为x元,
则年获利为
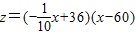
=
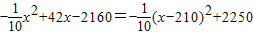
,
当z年获利为1840万时,
即z=1840+250=2090,
所以令
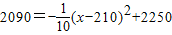
,
解得x
1=170,x
2=250,
当
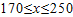
时,z≥2090,
∴第二年的销售单价应确定在不低于170元且不高于250元的范围内.
点评:此题考查一次函数和二次函数的性质及其应用,将实际问题转化为求函数最值问题,从而来解决实际问题,看似复杂其实比较简单.

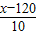 ,即:
,即: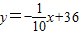 ,
,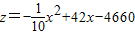 ;
;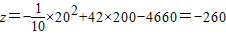
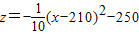
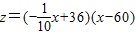
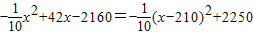 ,
,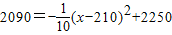 ,
,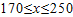 时,z≥2090,
时,z≥2090,

 同步轻松练习系列答案
同步轻松练习系列答案