
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6, ![]() .求BE的长.
.求BE的长.

【答案】(1)证明过程见解析;(2)2.5
【解析】试题分析:(1)连OD,OE,根据圆周角定理得到∠ADO+∠1=90°,而∠CDA=∠CBD,∠CBD=∠1,于是∠CDA+∠ADO=90°;(2)根据已知条件得到△CDA∽△CBD由相似三角形的性质得到![]() ,求得CD=4,由切线的性质得到BE=DE,BE⊥BC根据勾股定理列方程即可得到结论.
,求得CD=4,由切线的性质得到BE=DE,BE⊥BC根据勾股定理列方程即可得到结论.
试题解析:(1)连结OD, ∵OB=OD, ∴∠OBD=∠BDO, ∵∠CDA=∠CBD, ∴∠CDA=∠ODB,
又∵AB是⊙O的直径, ∴∠ADB=90°, ∴∠ADO+∠ODB=90°, ∴∠ADO+∠CDA=90°, 即∠CDO=90°,
∴OD⊥CD, ∵OD是⊙O半径, ∴CD是⊙O的切线
(2)∵∠C=∠C,∠CDA=∠CBD ∴△CDA∽△CBD ∴![]() ∵
∵![]() ,BC=6, ∴CD=4,
,BC=6, ∴CD=4,
∵CE,BE是⊙O的切线 ∴BE=DE,BE⊥BC ∴BE2+BC2=EC2,即BE2+62=(4+BE)2 解得:BE=2.5


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:
【题目】某家电商场将一款电视机按进价提高40%定价,再写上“八折酬宾”,结果每台电视机盈利不低于240元,则电视机的进价至少为每台________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图2的形状拼成一个正方形.
(1)图2中间的小正方形(即阴影部分)面积可表示为 .
(2)观察图2,请你写出三个代数式(m+n)2 , (m﹣n)2 , mn之间的等量关系式: .
(3)根据(2)中的结论,若x+y=﹣6,xy=2.75,则x﹣y= .
(4)有许多代数恒等式可以用图形的面积来表示.如图3所示,它表示了(2m+n)(m+n)=2m2+3mn+n2 . 试画出一个几何图形,使它的面积能表示为(m+n)(m+2n)=m2+3mn+2n2 . 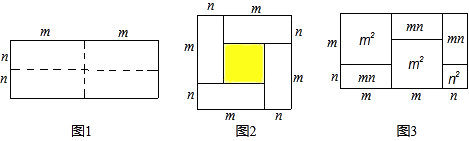
查看答案和解析>>
科目:初中数学 来源: 题型:
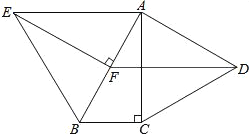
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE,已知∠ABC=60°,EF⊥AB,垂足为F,连接DF.
(1)求证:△ABC≌△EAF;
(2)试判断四边形EFDA的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家商店将某种服装按成本价每件a元提高50%标价,又以8折优惠卖出,则这种服装每件的售价是( )
A.0.8a元
B.0.4a元
C.1.2a元
D.1.5a元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一副三角板按如图所示叠放在一起,其中点B、D重合,若固定三角形AOB, 改变△ACD的位置(其中A点位置始终不变),使三角形ACD的一边与三角形AOB的某一边平行时,写出∠BAD的所有可能的值 . 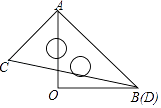
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方程x2+2x﹣3=0的解是( )
A. x1=1,x2=3 B. x1=1,x2=﹣3
C. x1=﹣1,x2=3 D. x1=﹣1,x2=﹣3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com