
”¾ĢāÄæ”æČēĶ¼ĖłŹ¾µÄŅęÖĒĶę¾ßÓÉŅ»æéÖ÷°åABŗĶŅ»øöÖ§³Å¼ÜCD×é³É£¬Ęä²ąĆęŹ¾ŅāĶ¼ČēĶ¼1ĖłŹ¾£¬²āµĆAB”ĶBD£¬AB=40cm£¬CD=25cm£¬µćCĪŖABµÄÖŠµć£®ĻÖĪŖĮĖ·½±ć¶łĶƲŁ×÷£¬Ščµ÷ÕūĶę¾ßµÄ°Ś·Å£¬½«ABČʵćBĖ³Ź±ÕėŠż×Ŗ£¬CDČʵćCŠż×Ŗ£¬Ķ¬Ź±µćD×öĖ®Ę½»¬¶Æ(ČēĶ¼2)£¬µ±µćC1µ½BDµÄ¾ąĄėĪŖ10cmŹ±Ķ£Ö¹ŌĖ¶Æ£¬ĒóµćA¾¹żµÄĀ·¾¶µÄ³¤ŗĶµćD»¬¶ÆµÄ¾ąĄė£®(½į¹ū±£ĮōÕūŹż£¬²Īæ¼Źż¾Ż£ŗ![]() ”Ö1£®732£¬
”Ö1£®732£¬ ![]() ”Ö4£®583£¬¦Š”Ö3£®142)
”Ö4£®583£¬¦Š”Ö3£®142)
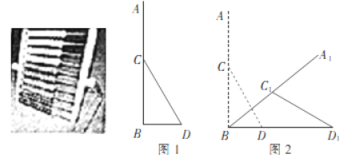
”¾“š°ø”æ42cm£¬25cm
”¾½āĪö”æ
Ź×ĻČĄūÓĆ¹“¹É¶ØĄķµĆ³öBDµÄ³¤£¬ŌŁ¹żµćC1×÷C1H”ĶBD1ÓŚµćH£¬½ų¶ųµĆ³öBH=10![]() cm£¬Ēó³ö”ĻABC1=60”ć£¬ĄūÓĆ»”³¤¹«Ź½Ēó³öµćA¾¹żµÄĀ·¾¶µÄ³¤£¬ŌŁĒó³öD1C1=25cm£¬C1H=10cm£¬½ų¶ųµĆ³öD1H”¢BD1µÄ³¤£¬¼“æÉµĆ³ö“š°ø£®
cm£¬Ēó³ö”ĻABC1=60”ć£¬ĄūÓĆ»”³¤¹«Ź½Ēó³öµćA¾¹żµÄĀ·¾¶µÄ³¤£¬ŌŁĒó³öD1C1=25cm£¬C1H=10cm£¬½ų¶ųµĆ³öD1H”¢BD1µÄ³¤£¬¼“æÉµĆ³ö“š°ø£®
”ßAB=40£¬µćCŹĒABµÄÖŠµć£¬
”ąBC=![]() AB=20cm£¬
AB=20cm£¬
”ßAB”ĶBD£¬
”ą”ĻCBD=90”ć£¬
ŌŚRt”÷BCDÖŠ£¬BC=20cm£¬DC=25cm£¬
”ąBD=![]() =
=![]() =15£Øcm£©£¬
=15£Øcm£©£¬
¹żµćC1×÷C1H”ĶBD1ÓŚµćH£¬

Ōņ”ĻC1HD=C1HD1=90”ć£¬
ŌŚRt”÷BC1HÖŠ£¬BC1=20cm£¬C1H=10cm£¬
”ą”ĻC1BH=30”ć£¬¹ŹBH=10![]() cm£¬
cm£¬
Ōņ”ĻABC1=60”ć£¬
¹ŹµćA¾¹żµÄĀ·¾¶µÄ³¤ĪŖ£ŗ![]() ”Ö42£Øm£©£¬
”Ö42£Øm£©£¬
ŌŚRt”÷D1C1HÖŠ£¬D1C1=25cm£¬C1H=10cm£¬
”ąD1H=![]() =
=![]() £Øcm£©£¬
£Øcm£©£¬
”ąBD1=BH+HD1=10![]() +5
+5![]() ”Ö17.32+22.915=40.235£Øcm£©£¬
”Ö17.32+22.915=40.235£Øcm£©£¬
”ąµćD»¬¶ÆµÄ¾ąĄėĪŖ£ŗBD1-BD=40.235-15=25.235”Ö25£Øcm£©£¬
“š£ŗµćD»¬¶ÆµÄ¾ąĄėĪŖ25m£¬µćA¾¹żµÄĀ·¾¶µÄ³¤ĪŖ42m£®


 ÓÅ°Ł·ÖæĪŹ±»„¶ÆĻµĮŠ“š°ø
ÓÅ°Ł·ÖæĪŹ±»„¶ÆĻµĮŠ“š°ø æŖŠÄĶÜדŌŖ×÷ŅµĻµĮŠ“š°ø
æŖŠÄĶÜדŌŖ×÷ŅµĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
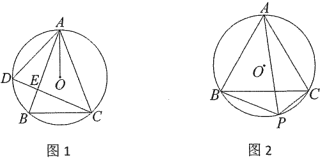
”¾ĢāÄæ”æµČŃü![]() ÖŠ£¬
ÖŠ£¬![]() £¬×÷
£¬×÷![]() µÄĶā½ÓŌ²”ŃO.
µÄĶā½ÓŌ²”ŃO.
£Ø1£©ČēĶ¼1£¬µć![]() ĪŖ
ĪŖ![]() ÉĻŅ»µć£Ø²»ÓėA”¢BÖŲŗĻ£©£¬Į¬½ÓAD”¢CD”¢AO£¬¼Ē
ÉĻŅ»µć£Ø²»ÓėA”¢BÖŲŗĻ£©£¬Į¬½ÓAD”¢CD”¢AO£¬¼Ē![]() Óė
Óė![]() µÄ½»µćĪŖ
µÄ½»µćĪŖ![]() .
.
¢ŁÉč![]() £¬Čō
£¬Čō![]() £¬ĒėÓĆŗ¬
£¬ĒėÓĆŗ¬![]() Óė
Óė![]() µÄŹ½×Ó±ķŹ¾
µÄŹ½×Ó±ķŹ¾![]() £»
£»
¢Śµ±![]() Ź±£¬Čō
Ź±£¬Čō![]() £¬Ēó
£¬Ēó![]() µÄ³¤£»
µÄ³¤£»
£Ø2£©ČēĶ¼2£¬µć![]() ĪŖ
ĪŖ![]() ÉĻŅ»µć£Ø²»ÓėB”¢CÖŲŗĻ£©£¬µ±BC=AB£¬AP=8Ź±£¬Éč
ÉĻŅ»µć£Ø²»ÓėB”¢CÖŲŗĻ£©£¬µ±BC=AB£¬AP=8Ź±£¬Éč![]() £¬Ēó
£¬Ēó![]() ĪŖŗĪÖµŹ±£¬
ĪŖŗĪÖµŹ±£¬![]() ÓŠ×ī“óÖµ£æ²¢ĒėÖ±½ÓŠ“³ö“ĖŹ±”ŃOµÄ°ė¾¶£®
ÓŠ×ī“óÖµ£æ²¢ĒėÖ±½ÓŠ“³ö“ĖŹ±”ŃOµÄ°ė¾¶£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¾Ż±ØµĄ£¬”°¹ś¼Ź¼ōµ¶ŹÆĶ·²¼Š»į”±ĢįŅ齫”°¼ōµ¶ŹÆĶ·²¼”±×÷ĪŖ°ĀŌĖ»į±ČČüĻīÄ森ijŠ£Ń§Éś»įĻėÖŖµĄŃ§Éś¶ŌÕāøöĢįŅéµÄĮĖ½ā³Ģ¶Č£¬Ė껜³éČ”²æ·Öѧɜ½ųŠŠĮĖŅ»“ĪĪŹ¾ķµ÷²é£¬²¢øł¾ŻŹÕ¼Æµ½µÄŠÅĻ¢½ųŠŠĮĖĶ³¼Ę£¬»ęÖĘĮĖĻĀĆęĮ½·łÉŠ²»ĶźÕūµÄĶ³¼ĘĶ¼£®ĒėÄćøł¾ŻĶ³¼ĘĶ¼ÖŠĖłĢį¹©µÄŠÅĻ¢½ā“šĻĀĮŠĪŹĢā£®
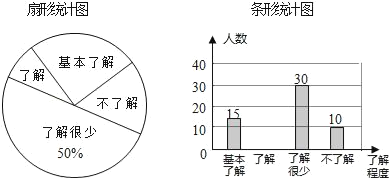
£Ø1£©½ÓŹÜĪŹ¾ķµ÷²éµÄѧɜ¹²ÓŠ”” ””Ćū£¬ÉČŠĪĶ³¼ĘĶ¼ÖŠ”°»ł±¾ĮĖ½ā”±²æ·ÖĖł¶ŌÓ¦ÉČŠĪµÄŌ²ŠÄ½ĒĪŖ”” ””£»Ēė²¹Č«ĢõŠĪĶ³¼ĘĶ¼£»
£Ø2£©ČōøĆŠ£¹²ÓŠŃ§Éś1200ČĖ£¬Ēėøł¾ŻÉĻŹöµ÷²é½į¹ū£¬¹Ą¼ĘøĆŠ£Ń§ÉśÖŠ¶Ō½«”°¼ōµ¶ŹÆĶ·²¼”±×÷ĪŖ°ĀŌĖ»į±ČČüĻīÄæµÄĢįŅé“ļµ½”°ĮĖ½ā”±”±ŗĶ”°»ł±¾ĮĖ½ā”±³Ģ¶ČµÄ×ÜČĖŹż£»
£Ø3£©”°¼ōµ¶ŹÆĶ·²¼”±±ČČüŹ±Ė«·½Ćæ“ĪČĪŅā³ö”°¼ōµ¶”±”¢”°ŹÆĶ·”±”¢”°²¼”±ÕāČżÖÖŹÖŹĘÖŠµÄŅ»ÖÖ£¬¹ęŌņĪŖ£ŗ¼ōµ¶Ź¤²¼£¬²¼Ź¤ŹÆĶ·£¬ŹÆĶ·Ź¤¼ōµ¶£¬ČōĖ«·½³öĻÖĻąĶ¬ŹÖŹĘ£¬ŌņĖć“ņĘ½£®ČōŠ”øÕŗĶŠ”Ć÷Į½ČĖÖ»±ČČüŅ»¾Ö£¬ĒėÓĆŹ÷דĶ¼»ņĮŠ±ķ·ØĒóĮ½ČĖ“ņĘ½µÄøÅĀŹ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŖ¼ÓĒæÖŠŠ”ѧɜ°²Č«½ĢÓż£¬Ä³Š£×éÖÆĮĖ”°·ĄÄēĖ®”±ÖŖŹ¶¾ŗČü£¬¶Ō±ķĻÖÓÅŅģµÄ°ą¼¶½ųŠŠ½±Ąų£¬Ń§Š£¹ŗĀņĮĖČōøÉø±Ę¹ÅŅĒņÅÄŗĶӚƫĒņÅÄ£¬¹ŗĀņ2ø±Ę¹ÅŅĒņÅÄŗĶ1ø±ÓšĆ«ĒņÅĹ²Šč116ŌŖ£»¹ŗĀņ3·łĘ¹ÅŅĒņÅÄŗĶ2·łÓšĆ«ĒņÅĹ²Šč204ŌŖ.
(1)Ēó¹ŗĀņ1ø±Ę¹ÅŅĒņÅÄŗĶ1ø±ÓšĆ«ĒņÅÄø÷Šč¶ąÉŁŌŖ£»
(2)ČōѧŠ£¹ŗĀņĘ¹ÅŅĒņÅÄŗĶӚƫĒņÅĹ²30·ł£¬ĒŅÖ§³ö²»³¬¹ż1480ŌŖ£¬Ōņ×ī¶ąÄܹ»¹ŗĀņ¶ąÉŁø±ÓšĆ«ĒņÅÄ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
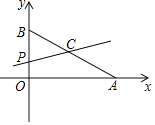
”¾ĢāÄæ”æČēĶ¼£¬Ę½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ŅŃÖŖµćA£Ø8£¬0£©ŗĶµćB£Ø0£¬6£©£¬µćCŹĒABµÄÖŠµć£¬µćPŌŚÕŪĻßAOBÉĻ£¬Ö±ĻßCP½Ų”÷AOB£¬ĖłµĆµÄČż½ĒŠĪÓė”÷AOBĻąĖĘ£¬ÄĒĆ“µćPµÄ×ų±źŹĒ_____£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖČēĶ¼£¬![]() £¬ĖüĆĒŅĄ“Ī½»Ö±Ļßa£¬bÓŚµćA”¢B”¢CŗĶµćD”¢E”¢F.
£¬ĖüĆĒŅĄ“Ī½»Ö±Ļßa£¬bÓŚµćA”¢B”¢CŗĶµćD”¢E”¢F.

£Ø1£©Čē¹ū![]() £¬
£¬![]() £¬
£¬![]() £¬ĒóDEµÄ³¤.
£¬ĒóDEµÄ³¤.
£Ø2£©Čē¹ū![]() £¬
£¬![]() £¬
£¬![]() £¬ĒóBEµÄ³¤.
£¬ĒóBEµÄ³¤.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
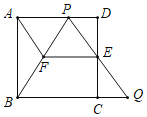
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ±ß³¤ĪŖlµÄÕż·½ŠĪABCDÖŠ£¬EŹĒ±ßCDµÄÖŠµć£¬µćPŹĒ±ßADÉĻŅ»µć£ØÓėµćA”¢D²»ÖŲŗĻ£©£¬ÉäĻßPEÓėBCµÄŃÓ³¤Ļß½»ÓŚµćQ£®
£Ø1£©ĒóÖ¤£ŗ![]() £»
£»
£Ø2£©¹żµćE×÷![]() ½»PBÓŚµćF£¬Į¬½įAF£¬µ±
½»PBÓŚµćF£¬Į¬½įAF£¬µ±![]() Ź±£¬¢ŁĒóÖ¤£ŗĖıߊĪAFEPŹĒĘ½ŠŠĖıߊĪ£»
Ź±£¬¢ŁĒóÖ¤£ŗĖıߊĪAFEPŹĒĘ½ŠŠĖıߊĪ£»
¢ŚĒėÅŠ¶ĻĖıߊĪAFEPŹĒ·ńĪŖĮāŠĪ£¬²¢ĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬DE”ĪBC£¬EF”ĪAB£®
£Ø1£©ĒóÖ¤£ŗ”÷ADE”×”÷EFC£»
£Ø2£©Čē¹ūAB=6£¬AD=4£¬Ēó![]() µÄÖµ.
µÄÖµ.
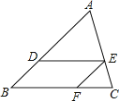
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ņ»“ĪŗÆŹży£½©x+bµÄĶ¼ĻóÓė·“±ČĄżŗÆŹży£½![]() µÄĶ¼Ļó½»ÓŚA”¢BĮ½µć£¬ĒŅAµć×ų±źĪŖ£Ø©2£¬1£©£¬Ņ»“ĪŗÆŹż½»xÖįÓŚµćC£®
µÄĶ¼Ļó½»ÓŚA”¢BĮ½µć£¬ĒŅAµć×ų±źĪŖ£Ø©2£¬1£©£¬Ņ»“ĪŗÆŹż½»xÖįÓŚµćC£®
£Ø1£©ŹŌČ·¶ØÉĻŹö·“±ČĄżŗÆŹżŗĶŅ»“ĪŗÆŹżµÄ±ķ“ļŹ½£»
£Ø2£©Ēó”÷AOBµÄĆ껿£»
£Ø3£©Ö±½ÓŠ“³öŹ¹·“±ČĄżŗÆŹż“óÓŚŅ»“ĪŗÆŹżµÄxµÄȔֵ·¶Ī§£®

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com