
【题目】如图是用长度相等的小棒按一定规律摆成的一组图案.
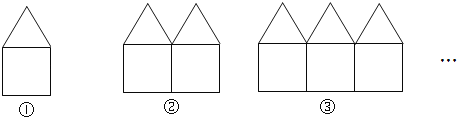
(1)第1个图案中有6根小棒;第2个图案中有 根小棒;第3个图案中有 根小棒;
(2)第n个图案中有多少根小棒?
(3)第25个图案中有多少根小棒?
(4)是否存在某个符合上述规律的图案,由2032根小棒摆成?如果有,指出是滴几个图案;如果没有,请说明理由.
【答案】(1)11 , 16 (2)![]() (3)126 (4)不存在, 理由:令
(3)126 (4)不存在, 理由:令![]() ,得出n=406.2,不是整数,故不存在符合上述规律的图案,由2032根小棒摆成.
,得出n=406.2,不是整数,故不存在符合上述规律的图案,由2032根小棒摆成.
【解析】
(1)(2)由图可知:第1个图案中有5+1=6根小棒,第2个图案中有2×5+2-1=11根小棒,第3个图案中有3×5+3-2=16根小棒,…由此得出第n个图案中有5n+n-(n-1)=5n+1根小棒;
(3)把数据代入(2)中的规律求得答案即可;
(4)利用(2)中的规律建立方程求得答案即可.
(1)第2个图案中有11根小棒;第3个图案中有16根小棒;
(2)由图可知:第1个图案中有5+1=6根小棒,第2个图案中有2×5+2-1=11根小棒,第3个图案中有3×5+3-2=16根小棒,…,因此第n个图案中有5n+n-(n-1)=5n+1根;
(3)令n=25,得出![]() ,故第25个图案中有126根小棒;
,故第25个图案中有126根小棒;
(4)令![]() ,得出n=406.2,不是整数,故不存在符合上述规律的图案,由2032根小棒摆成.
,得出n=406.2,不是整数,故不存在符合上述规律的图案,由2032根小棒摆成.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:
【题目】某网络约车公司近期推出了“520专享”服务计划,即要求公司员工做到“5星级服务、2分钟响应、0客户投诉”,为进一步提升服务品质,公司监管部门决定了解“单次营运里程”的分布情况.老王收集了本公司的5000个“单次营运里程”数据,这些里程数据均不超过25(千米),他从中随机抽取了200个数据作为一个样本,整理、统计结果如下表,并绘制了不完整的频数分布直方图.
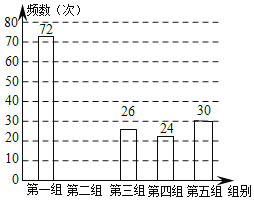
组别 | 单次营运里程“x”(千米) | 频数 |
第一组 | 0<x≤5 | 72 |
第二组 | 5<x≤10 | a |
第三组 | 10<x≤15 | 26 |
第四组 | 15<x≤20 | 24 |
第五组 | 20<x≤25 | 30 |
根据以上信息,解答下列问题:
(1)表中a= ,样本中“单次营运里程”不超过15千米的频率为 ;
(2)请把频数分布直方图补充完整;
(3)估计该公司5000个“单次营运里程”超过20千米的次数.(写出解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学九年级开展“社会主义核心价值观”演讲比赛活动,九(1)班、九(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出5名选手的复赛成绩(满分100分)如图所示.

根据图中数据解决下列问题:
(1)九(1)班复赛成绩的众数是 分,九(2)班复赛成绩的中位数是 分;
(2)请你求出九(1)班和九(2)班复赛的平均成绩和方差,并说明哪个班的成绩更稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:(﹣2)﹣1﹣|﹣![]() |+(
|+(![]() ﹣1)0+cos45°.
﹣1)0+cos45°.
(2)已知m2﹣5m﹣14=0,求(m﹣1)(2m﹣1)﹣(m+1)2+1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
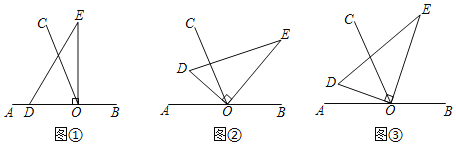
【题目】如图,以直线AB上一点O为端点作射线OC,使∠AOC=65°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图①,若直角三角板DOE的一边OD放在射线OA上,则∠COE= ;
(2)如图②,将直角三角板DOE绕点O顺时针方向转动到某个位置,若OC恰好平分∠AOE,求∠COD的度数;
(3)如图③,将直角三角板DOE绕点O任意转动,如果OD始终在∠AOC的内部,试猜想∠AOD和∠COE有怎样的数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A,B两点在数轴上,点A在原点O的左边,表示的数为﹣10,点B在原点的右边,且BO=3AO.点M以每秒3个单位长度的速度从点A出发向右运动.点N以每秒2个单位长度的速度从点O出发向右运动(点M,点N同时出发).
(1)数轴上点B对应的数是 ,点B到点A的距离是 ;
(2)经过几秒,原点O是线段MN的中点?
(3)经过几秒,点M,N分别到点B的距离相等?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
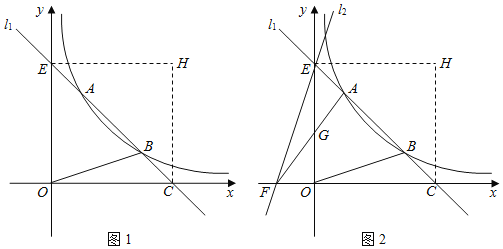
【题目】如图1,直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,已知点
,已知点![]() 、点
、点![]() .
.
(1)求直线![]() 和双曲线的解析式;
和双曲线的解析式;
(2)将![]() 沿直线
沿直线![]() 翻折,点
翻折,点![]() 落在第一象限内的点
落在第一象限内的点![]() 处,直接写出点
处,直接写出点![]() 的坐标;
的坐标;
(3)如图2,过点![]() 作直线
作直线![]() 交
交![]() 轴的负半轴于点
轴的负半轴于点![]() ,连接
,连接![]() 交
交![]() 轴于点
轴于点![]() ,且
,且![]() 的面积与
的面积与![]() 的面积相等.
的面积相等.
①求直线![]() 的解析式;
的解析式;
②在直线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,请直接写出所有符合条件的点
?若存在,请直接写出所有符合条件的点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
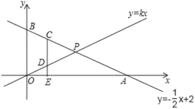
【题目】在平面直角坐标系中,一次函数![]() 的图象交
的图象交![]() 轴、
轴、![]() 轴分别于
轴分别于![]() 两点,交直线
两点,交直线![]() 于
于![]() 。
。
(1)求点![]() 的坐标;
的坐标;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,![]() 是线段
是线段![]() 上一点,
上一点,![]() 轴于
轴于![]() ,交
,交![]() 于
于![]() ,若
,若![]() ,求
,求![]() 点的坐标。
点的坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com