
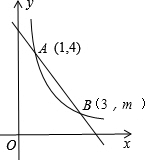
 如图,在直角坐标系xOy中,一次函数y1=k1x+b的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于A(1,4),B(3,m)两点.
如图,在直角坐标系xOy中,一次函数y1=k1x+b的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于A(1,4),B(3,m)两点.分析 (1)把A点坐标代入y2=$\frac{{k}_{2}}{x}$,求得反比例函数解析式,把x=3代入反比例函数解析式求出m的值,得到点B的坐标,把A,B坐标代入一次函数即可求得解析式;
(2)已知A、B两点的坐标,观察图象即可得到y1与y2的大小关系;
(3)设直线AB:y1=-$\frac{4}{3}$x+$\frac{16}{3}$与x轴交于点C,令y=0,求得C点坐标,将△AOB的面积化为两个三角形的面积之差.
解答 解:(1)∵点A(1,4)在反比例函数y2=$\frac{{k}_{2}}{x}$的图象上,
∴k2=1×4=4,
∴反比例函数的解析式为:y2=$\frac{4}{x}$.
∵B(3,m)在双曲线y2=$\frac{4}{x}$上,
∴m=$\frac{4}{3}$,
∴B(3,$\frac{4}{3}$).
∵A(1,4)、B(3,$\frac{4}{3}$)在直线y1=k1x+b上,
∴$\left\{\begin{array}{l}{{k}_{1}+b=4}\\{3{k}_{1}+b=\frac{4}{3}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{k}_{1}=-\frac{4}{3}}\\{b=\frac{16}{3}}\end{array}\right.$,
故一次函数的解析式为:y1=-$\frac{4}{3}$x+$\frac{16}{3}$;
(2)∵A(1,4)、B(3,$\frac{4}{3}$),
∴结合图象可得:
①当x=1或x=3时,y1=y2;
②当0<x<1或x>3时,y1<y2;
③当1<x<3时,y1>y2;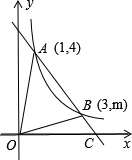 (3)设直线AB:y1=-$\frac{4}{3}$x+$\frac{16}{3}$与x轴交于点C,
(3)设直线AB:y1=-$\frac{4}{3}$x+$\frac{16}{3}$与x轴交于点C,
令y=0,得x=4,
所以C(4,0),
则S△AOB=S△AOC-S△COB
=$\frac{1}{2}$×4×4-$\frac{1}{2}$×4×$\frac{4}{3}$
=8-$\frac{8}{3}$
=$\frac{16}{3}$.
点评 本题考查了反比例函数和一次函数的交点问题,以及用待定系数法求反比例函数和一次函数的解析式,三角形的面积,是基础知识要熟练掌握.


 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:初中数学 来源: 题型:选择题
| A. | $\root{3}{-3}=-\root{3}{-3}$ | B. | $\root{3}{-3}=\root{3}{3}$ | C. | $\root{3}{-3}=\root{3}{{|{-3}|}}$ | D. | $\root{3}{-3}=-\root{3}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
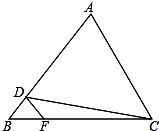 如图,在△ABC中,D、F分别是AB、BC上的点,且DF∥AC,若S△BDF:S△DFC=1:4,则S△BDF:S△DCA=( )
如图,在△ABC中,D、F分别是AB、BC上的点,且DF∥AC,若S△BDF:S△DFC=1:4,则S△BDF:S△DCA=( )| A. | 1:16 | B. | 1:18 | C. | 1:20 | D. | 1:24 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
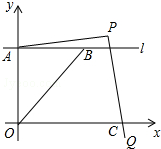 如图,在平面直角坐标系中,直线l平行x轴,交y轴于点A,第一象限内的点B在l上,连结OB,动点P满足∠APQ=90°,PQ交x轴于点C.
如图,在平面直角坐标系中,直线l平行x轴,交y轴于点A,第一象限内的点B在l上,连结OB,动点P满足∠APQ=90°,PQ交x轴于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
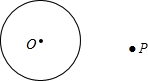 我们在探索“圆”时,学习了圆周角与圆心角的关系定理的推论“直径所对的圆周角是直角”.请利用此推论,完成下面的尺规作图.如图,点P是⊙O外的一点,用圆规和直尺过点P作出⊙O的切线.(要求:不写作法,保留作图痕迹,写出结论)
我们在探索“圆”时,学习了圆周角与圆心角的关系定理的推论“直径所对的圆周角是直角”.请利用此推论,完成下面的尺规作图.如图,点P是⊙O外的一点,用圆规和直尺过点P作出⊙O的切线.(要求:不写作法,保留作图痕迹,写出结论)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 分组 | 49.5~59.5 | 59.5~69.5 | 69.5~79.5 | 79.5~89.5 | 89.5~100.5 | 合计 |
| 频数 | 2 | A | 20 | 16 | 4 | 50 |
| 频率 | 0.04 | 0.16 | 0.40 | 0.32 | B | 1 |
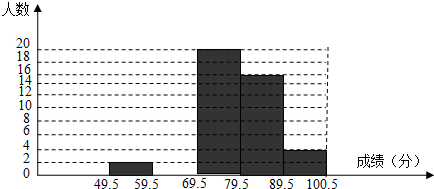
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
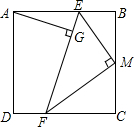 已知,在正方形ABCD中,M是边BC中点,E是边AB上的一个动点,MF⊥ME,交射线CD于点F,AB=4,当DF=1时,求点A到直线EF的距离.
已知,在正方形ABCD中,M是边BC中点,E是边AB上的一个动点,MF⊥ME,交射线CD于点F,AB=4,当DF=1时,求点A到直线EF的距离.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com